【题目】如图,在△ABC中,AB=6,AC=10,AD是BC边上的中线,且AD=4,延长AD到点E,使DE=AD,连接CE.
(1)求证:△AEC是直角三角形.
(2)求BC边的长.

参考答案:
【答案】(1)证明见解析;(2)BC=![]() .
.
【解析】
(1)首先证明△ABD≌△ECD,推出EC=AB=6,由AE2+EC2=AC2,推出△AEC是直角三角形.
(2)在Rt△CDE中,求出CD,根据BC=2CD即可解决问题.
(1)∵AD是BC边上的中线
∴BD=CD
又∵DE=AD, ∠ADB=∠CDE
∴△ABD≌△ECD,
∴EC=AB=6,
∵AE=8 ,AC=10
∴△AEC 中,AE2+EC2=AC2
∴△AEC是直角三角形.
(2)在Rt△CDE中,CD2=CE2+DE2=62+42=52
∴CD=![]()
∴BC=2CD=![]() .
.
-
科目: 来源: 题型:
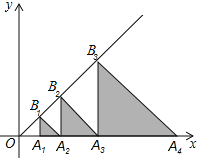
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点A1,A2,A3,…分别在x轴上,点B1,B2,B3,…分别在直线y=x上,△OA1B1,△B1A1A2,△B1B2A2,△B2A2A3,△B2B3A3…,都是等腰直角三角形,如果OA1=1,则点A2019的坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三角形BCO是三角形BAO经过某种变换得到的.
(1)写出A,C的坐标;
(2)图中A与C的坐标之间的关系是什么?
(3)如果三角形AOB中任意一点M的坐标为(x,y),那么它的对应点N的坐标是什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】有下列结论:
 平分弦的直径垂直于弦;
平分弦的直径垂直于弦; 圆周角的度数等于圆心角的一半;
圆周角的度数等于圆心角的一半; 等弧所对的圆周角相等;
等弧所对的圆周角相等; 经过三点一定可以作一个圆;
经过三点一定可以作一个圆; 三角形的外心到三边的距离相等;
三角形的外心到三边的距离相等; 垂直于半径的直线是圆的切线.
垂直于半径的直线是圆的切线.其中正确的个数为( )
A.
 个 B.
个 B.  个 C.
个 C.  个 D.
个 D.  个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=
 ,y=
,y=
(1)求x2+xy+y2.
(2)若x的小数部分为a,y的整数部分为b,求ax+by的平方根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为
为 的直径
的直径 延长线上的一点,
延长线上的一点, 与
与 相切,切点为
相切,切点为 ,点
,点 是
是 上一点,连接
上一点,连接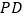 .已知
.已知 .下列结论:
.下列结论: 与
与 相切;
相切; 四边形
四边形 是菱形;
是菱形; ;
; .
.其中正确的个数为( )

A.
 个 B.
个 B.  个 C.
个 C.  个 D.
个 D.  个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b的图象与y=x-1的图象平行,且经过点(2,6).
(1)求一次函数y=kx+b的表达式.
(2)求这个一次函数y=kx+b与坐标轴的两个交点坐标,并在直角坐标系中画出这个函数的图象.

相关试题

