【题目】(1)如图,在△ABC中,∠ABC、∠ACB的平分线相交于F,过F作DE∥BC,分别交AB、AC于点D、E.判断DE=DB+EC是否成立?为什么?

(2)如图,若点F是∠ABC的平分线和外角∠ACG的平分线的交点,其他条件不变,请猜想线段DE、DB、EC之间有何数量关系?
证明你的猜想。

参考答案:
【答案】(1)成立,证明见解析.(2)证明见解析.
【解析】试题分析: ![]() 根据平行线的性质和角平分线的性质,得出
根据平行线的性质和角平分线的性质,得出![]() 和
和![]() 是等腰三角形,通过等量代换即可得出结论.
是等腰三角形,通过等量代换即可得出结论.
![]() 同
同![]() ,只要求出
,只要求出![]() 和
和![]() 是等腰三角形即可.
是等腰三角形即可.
试题解析:(1)成立;
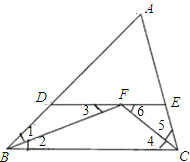
∵△ABC中BF、CF平分∠ABC、∠ACB,
∴∠1=∠2,∠5=∠4.
∵DE∥BC,∴∠2=∠3,∠4=∠6.
∴∠1=∠3,∠6=∠5.
根据在同一个三角形中,等角对等边的性质,可知:BD=DF,EF=CE.
∴DE=DF+EF=BD+CE.
故成立.
(2)∵BF分∠ABC,
∴∠DBF=∠FBC.
![]()
∴∠DFB=∠FBC.
∴∠ABF=∠DFB,
∴BD=DF.
∵CF平分∠ACG,
∴∠ACF=∠FCG.
![]()
∴∠DFC=∠FCG.
∴∠ACF=∠DFC,
∴CE=EF.
∴EF+DE=DF,即DE+EC=BD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图△ADF和△BCE中,∠A=∠B,点D、E、F、C在同﹣直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF。

(1)请用其中两个关系式作为条件,另一个作为结论,写出所有你认为正确的命题.(用序号写出命题书写形式,如:如果①、②,那么③)
(2)选择(1)中你写出的一个命题,说明它正确的理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种品牌服装平均每天销售20件,每件盈利44元.销售过程中发现,在每件降价不超过10元的情况下,若每件降价1元,每天可多售5件.
(1)若每件降价2元,则每天售出 件,共盈利 元;
(2)如果销售这种品牌的服装每天要盈利2380元,求每件应降价多少元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:在△ABC中,AC=BC=4,∠ACB=120°,将一块足够大的直角三角尺PMN(∠M=90°,∠MPN=30°)按如图放置,顶点P在线段AB上滑动,三角尺的直角边PM始终经过点C,并且与CB的夹角∠PCB=α,斜边PN交AC于点D.
(1)当PN∥BC时,判断△ACP的形状,并说明理由;
(2)点P在滑动时,当AP长为多少时,△ADP与△BPC全等,为什么?
(3)点P在滑动时,△PCD的形状可以是等腰三角形吗?若可以,请求出夹角α的大小;若不可以,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y1=﹣
 x﹣1与反比例函数y2=
x﹣1与反比例函数y2= 的图象交于点A(﹣4,m).
的图象交于点A(﹣4,m).(1)观察图象,在y轴的左侧,当y1>y2时,请直接写出x的取值范围;
(2)求出反比例函数的解析式.
(3)求直线与双曲线的另一个交点坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若|x﹣1|+(x+y+2)2=0,则x2+y2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
A. B分别为x轴、y轴正半轴上两动点,∠BAO的平分线与∠OBA的外角平分线所在直线交于点C,则∠C的度数随A、B运动的变化情况正确的是
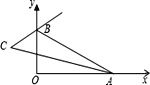
A.点B不动,在点A向右运动的过程中,∠C的度数逐渐减小
B. 点A不动,在点B向上运动的过程中,∠C的度数逐渐减小
C. 在点A向左运动,点B向下运动的过程中,∠C的度数逐渐增大
D. 在点A、B运动的过程中,∠C的度数不变
相关试题

