【题目】一次函数y1=﹣![]() x﹣1与反比例函数y2=
x﹣1与反比例函数y2=![]() 的图象交于点A(﹣4,m).
的图象交于点A(﹣4,m).
(1)观察图象,在y轴的左侧,当y1>y2时,请直接写出x的取值范围;
(2)求出反比例函数的解析式.
(3)求直线与双曲线的另一个交点坐标.

参考答案:
【答案】(1)当x<﹣4时,y1>y2;(2)反比例函数的解析式为y=﹣![]() ;;(3)直线与双曲线的另一个交点坐标为(2,﹣2)
;;(3)直线与双曲线的另一个交点坐标为(2,﹣2)
【解析】
试题分析:(1)根据图象结合交点坐标即可求得.
(2)先求出m,得出点A的坐标,求出k的值即可;
(3)由直线和反比例函数关系式组成方程组,解方程组即可.
试题解析:(1)根据图象得:当x<﹣4时,y1>y2
(2)把A(﹣4,m)代入一次函数y1=﹣![]() x﹣1得:m=1,
x﹣1得:m=1,
∴A(﹣4,1),
把A(﹣4,1)代入反比例函数y2=![]() 得:k=﹣4,
得:k=﹣4,
∴反比例函数的解析式为y=﹣![]() .
.
(3)解方程组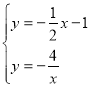 得:
得:![]() 或
或![]() ,∵A(﹣4,1),
,∵A(﹣4,1),
∴直线与双曲线的另一个交点坐标为(2,﹣2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种品牌服装平均每天销售20件,每件盈利44元.销售过程中发现,在每件降价不超过10元的情况下,若每件降价1元,每天可多售5件.
(1)若每件降价2元,则每天售出 件,共盈利 元;
(2)如果销售这种品牌的服装每天要盈利2380元,求每件应降价多少元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:在△ABC中,AC=BC=4,∠ACB=120°,将一块足够大的直角三角尺PMN(∠M=90°,∠MPN=30°)按如图放置,顶点P在线段AB上滑动,三角尺的直角边PM始终经过点C,并且与CB的夹角∠PCB=α,斜边PN交AC于点D.
(1)当PN∥BC时,判断△ACP的形状,并说明理由;
(2)点P在滑动时,当AP长为多少时,△ADP与△BPC全等,为什么?
(3)点P在滑动时,△PCD的形状可以是等腰三角形吗?若可以,请求出夹角α的大小;若不可以,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,在△ABC中,∠ABC、∠ACB的平分线相交于F,过F作DE∥BC,分别交AB、AC于点D、E.判断DE=DB+EC是否成立?为什么?

(2)如图,若点F是∠ABC的平分线和外角∠ACG的平分线的交点,其他条件不变,请猜想线段DE、DB、EC之间有何数量关系?
证明你的猜想。

-
科目: 来源: 题型:
查看答案和解析>>【题目】若|x﹣1|+(x+y+2)2=0,则x2+y2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
A. B分别为x轴、y轴正半轴上两动点,∠BAO的平分线与∠OBA的外角平分线所在直线交于点C,则∠C的度数随A、B运动的变化情况正确的是
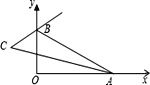
A.点B不动,在点A向右运动的过程中,∠C的度数逐渐减小
B. 点A不动,在点B向上运动的过程中,∠C的度数逐渐减小
C. 在点A向左运动,点B向下运动的过程中,∠C的度数逐渐增大
D. 在点A、B运动的过程中,∠C的度数不变
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx﹣3(a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线y=﹣
 x+1与y轴交于点D.
x+1与y轴交于点D.(1)求抛物线的解析式;
(2)证明:△DBO∽△EBC;
(3)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标,若不存在,请说明理由.

相关试题

