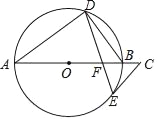
【题目】如图,AB是⊙O的直径,点D,E在⊙O上,∠A=2∠BDE,点C在AB的延长线上,∠C=∠ABD.
(1)求证:CE是⊙O的切线;
(2)若BF=2,EF=![]() ,求⊙O的半径长.
,求⊙O的半径长.
参考答案:
【答案】(1)见解析;(2)![]()
【解析】分析:(1)连接OE,首先得出△ABD∽△OCE,进而推出∠OCE=90°,即可得到结论;
(2)连接BE,得出△OBE∽△EBF,再利用相似三角形的性质得出OB的长,即可得到结论.
详解:(1)证明:连接OE,
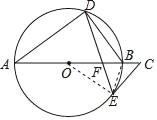
则∠BOE=2∠BDE,又∠A=2∠BDE,
∴∠BOE=∠A,
∵∠C=∠ABD,∠A=∠BOE,
∴△ABD∽△OCE
∴∠ADB=∠OEC,
又∵AB是直径,
∴∠OEC=∠ADB=90°
∴CE与⊙O相切;
(2)连接EB,则∠A=∠BED,
∵∠A=∠BOE,
∴∠BED=∠BOE,
在△BOE和△BEF中,
∠BEF=∠BOE,∠EBF=∠OBE,
∴△OBE∽△EBF,
∴![]() ,则
,则![]() ,
,
∵OB=OE,
∴EB=EF,
∴![]() ,
,
∵BF=2,EF=![]() ,
,
∴![]() ,
,
∴OB=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为培养学生良好学习习惯,某学校计划举行一次“整理错题集”的展示活动,对该校部分学生“整理错题集”的情况进行了一次抽样调查,根据收集的数据绘制了下面不完整的统计图表.
整理情况
频数
频率
非常好
0.21
较好
70
0.35
一般
m
不好
36
请根据图表中提供的信息,解答下列问题:
(1)本次抽样共调查了 名学生;
(2)m= ;
(3)该校有1500名学生,估计该校学生整理错题集情况“非常好”和“较好”的学生一共约多少名?
(4)某学习小组4名学生的错题集中,有2本“非常好”(记为A1、A2),1本“较好”(记为B),1本“一般”(记为C),这些错题集封面无姓名,而且形状、大小、颜色等外表特征完全相同,从中抽取一本,不放回,从余下的3本错题集中再抽取一本,请用“列表法”或“画树形图”的方法求出两次抽到的错题集都是“非常好”的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读与理解:
如图,一只甲虫在5×5的方格(每个方格边长均为1)上沿着网格线爬行.若我们规定:在如图网格中,向上(或向右)爬行记为“+”,向下(或向左)爬行记为“﹣”,并且第一个数表示左右方向,第二个数表示上下方向.
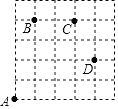
例如:从A到B记为:A→B(+1,+4),从D到C记为:D→C(﹣1,+2).
思考与应用:
(1)图中B→C( , )C→D( , )
(2)若甲虫从A到P的行走路线依次为:(+3,+2)→(+1,+3)→(+1,﹣2),请在图中标出P的位置.
(3)若甲虫的行走路线为A→(+1,+4)→(+2,0)→(+1,﹣2)→(﹣4,﹣2),请计算该甲虫走过的总路程S.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板(∠M=30°)的直角项点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.

(1)将图1中的三角板绕点O以每秒5°的速度沿逆时针方向旋转一周.如图2,经过t秒后,ON落在OC边上,则t= 秒(直接写结果).
(2)在(1)的条件下,若三角板继续转动,同时射线OC也绕O点以每秒10°的速度沿逆时针方向旋转一周,当OC转动9秒时,求∠MOC的度数.
(3)在(2)的条件下,它们继续运动多少秒时,∠MOC=35°?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下面左边
 方格中,都有两个形状、大小相同的直角三角形①、②,它们的顶点都在小正方形的顶点处(在方格中,三个顶点都在小正方形的顶点处的三角形叫做格点三角形).图中只有直角三角形①可以运动.按下列要求在右边的备用图中画出运动后的图形.
方格中,都有两个形状、大小相同的直角三角形①、②,它们的顶点都在小正方形的顶点处(在方格中,三个顶点都在小正方形的顶点处的三角形叫做格点三角形).图中只有直角三角形①可以运动.按下列要求在右边的备用图中画出运动后的图形.(注:一个
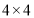 方格中只画一种情况,给出的备用图不一定全用,不够可添加)
方格中只画一种情况,给出的备用图不一定全用,不够可添加)(1)如图一,只通过平移直角三角形①,使平移后的图形与直角三角形②成旋转对称图形,请你画出所有与三角形②成旋转对称的格点三角形,并分别写出平移的方向及距离.
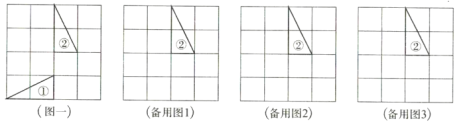
(2)如图二,只通过旋转直角三角形①(绕着它的顶点),使旋转后的图形与直角三角形②成轴对称图形,请你画出所有与三角形②成轴对称的格点三角形,并分别写出旋转的方向及旋转角,在图中标出旋转中心
 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】七年级一班某次数学测验的优秀成绩为80分,数学老师以优秀成绩为基准,记作0,把小龙、小聪、小梅、小莉、小刚这五位同学的成绩简记为+10,–15,0,+20,–2.问这五位同学的实际成绩分别是多少分?优秀率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:我们把三角形被一边中线分成的两个三角形叫做“友好三角形”.
性质:如果两个三角形是“友好三角形”,那么这两个三角形的面积相等.
理解:如图①,在△ABC中,CD是AB边上的中线,那么△ACD和△BCD是“友好三角形”,并且S△ACD=S△BCD.
应用:如图②,在矩形ABCD中,AB=4,BC=6,点E在AD上,点F在BC上,AE=BF,AF与BE交于点O.
(1)求证:△AOB和△AOE是“友好三角形”;
(2)连接OD,若△AOE和△DOE是“友好三角形”,求四边形CDOF的面积.
探究:在△ABC中,∠A=30°,AB=4,点D在线段AB上,连接CD,△ACD和△BCD是“友好三角形”,将△ACD沿CD所在直线翻折,得到△A′CD,若△A′CD与△ABC重合部分的面积等于△ABC面积的
 ,请直接写出△ABC的面积.
,请直接写出△ABC的面积.
相关试题

