【题目】某花圃用花盆培育某种花苗,经过试验发现每盆的盈利与每盆的株数构成一定的关系,每盆植入3株时,平均单株盈利3元,以同样的栽培条件,若每盆增加1株,平均单株盈利就减少0.5元,要使每盆的盈利达到10元,每盆应该植多少株? 小明的解法如下:
解:设每盆花苗增加x株,则每盆花苗有(x+3)株,平均单株盈利为(3﹣0.5x)元,
由题意得(x+3)(3﹣0.5x)=10,
化简,整理得:x2﹣3x+2=0
解这个方程,得:x1=1,x2=2,
答:要使每盆的盈利达到10元,每盆应该植入4株或5株.
(1)本题涉及的主要数量有每盆花苗株数,平均单株盈利,每盆花苗的盈利等,请写出两个不同的等量关系: .
(2)请用一种与小明不相同的方法求解上述问题.
参考答案:
【答案】
(1)平均单株盈利×每盆株数=每盆盈利,平均单株盈利=3﹣0.5×每盆增加的株数
(2)解:解法1(列表法)
每盆植入株数 | 平均单株盈利(元) | 每盆盈利(元) |
3 | 3 | 9 |
4 | 2.5 | 10 |
5 | 2 | 10 |
6 | 1.5 | 9 |
7 | 1 | 7 |
答:要使每盆的盈利达到10元,每盆应该植入4株或5株;
解法2(图象法)
如图,纵轴表示平均单株盈利,横轴表示株数,则相应长方形面积表示每盆盈利.
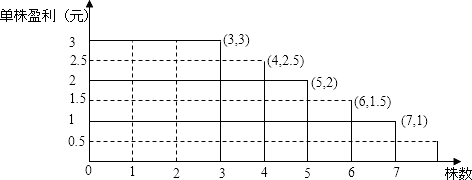
从图象可知,每盆植入4株或5株时,相应长方形面积都是10
答:要使每盆的盈利达到10元,每盆应该植入4株或5株.
解法3(函数法)
解:设每盆花苗增加x,每盆的盈利为y元,根据题意得可得:y=(x+3)(3﹣0.5x),
当y=10时,(x+3)(3﹣0.5x)=10,
解这个方程得:x1=1,x2=2,
答:要使每盆的盈利达到10元,每盆应该植入4或5株;
解法4(列分式方程)
解:设每盆花苗增加x株时,每盆盈利10元,根据题意,得:
![]() ,
,
解这个方程得:x1=1,x2=2,
经检验,x1=1,x2=2都是所列方程的解,
答:要使每盆的盈利达到10元,每盆应该植入4或5株
【解析】解:(1)平均单株盈利×每盆株数=每盆盈利, 平均单株盈利=3﹣0.5×每盆增加的株数;(1)根据题意可写出平均单株盈利×株数=每盆盈利;平均单株盈利=3﹣0.5×每盆增加的株数.(2)除了方程法,可用列表法,图象法和函数法,同学们可选择自己喜欢的方法看看.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面一段文字:
问题:
 能化为分数形式吗?
能化为分数形式吗?探求:步骤①设
 ,步骤②
,步骤② ,
,步骤③
 ,则
,则 ,
,步骤④
 ,解得:
,解得: .
.根据你对这段文字的理解,回答下列问题:
(1)步骤①到步骤②的依据是什么;
(2)仿照上述探求过程,请你尝试把
 化为分数形式:
化为分数形式:(3)请你将
 化为分数形式,并说明理由.
化为分数形式,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量? 操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验,摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中,再继续.
活动结果:摸球实验活动一共做了50次,统计结果如下表:球的颜色
无记号
有记号
红色
黄色
红色
黄色
摸到的次数
18
28
2
2
推测计算:由上述的摸球实验可推算:
(1)盒中红球、黄球各占总球数的百分比分别是多少?
(2)盒中有红球多少个? -
科目: 来源: 题型:
查看答案和解析>>【题目】在(1)
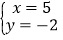 (2)
(2) 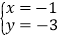 (3)
(3) 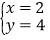 (4)
(4) 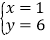 中,________是方程7x-3y=2的解;________是方程2x+y=8的解;________是方程组
中,________是方程7x-3y=2的解;________是方程2x+y=8的解;________是方程组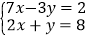 的解.(填序号)
的解.(填序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,连接EC.
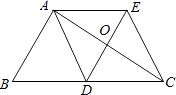
(1)求证:AD=EC;
(2)当∠BAC=90°时,求证:四边形ADCE是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC是一张等腰直角三角形纸板,∠C=90°,AC=BC=2,
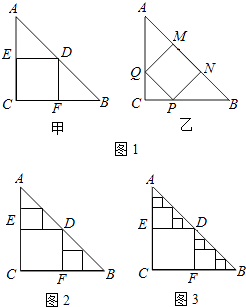
(1)要在这张纸板中剪出一个尽可能大的正方形,有甲、乙两种剪法(如图1),比较甲、乙两种剪法,哪种剪法所得的正方形面积大?请说明理由.
(2)图1中甲种剪法称为第1次剪取,记所得正方形面积为s1;按照甲种剪法,在余下的△ADE和△BDF中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为s2(如图2),则s2=;再在余下的四个三角形中,用同样方法分别剪取正方形,得到四个相同的正方形,称为第3次剪取,并记这四个正方形面积和为s3 , 继续操作下去…,则第10次剪取时,s10=;
(3)求第10次剪取后,余下的所有小三角形的面积之和. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两直线l1 , l2分别经过点A(1,0),点B(﹣3,0),并且当两直线同时相交于y正半轴的点C时,恰好有l1⊥l2 , 经过点A、B、C的抛物线的对称轴与直线l1交于点K,如图所示.
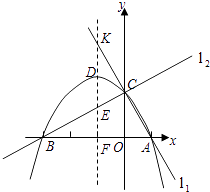
(1)求点C的坐标,并求出抛物线的函数解析式;
(2)抛物线的对称轴被直线l1 , 抛物线,直线l2和x轴依次截得三条线段,问这三条线段有何数量关系?请说明理由;
(3)当直线l2绕点C旋转时,与抛物线的另一个交点为M,请找出使△MCK为等腰三角形的点M,简述理由,并写出点M的坐标.
相关试题

