【题目】阅读下面一段文字:
问题:![]() 能化为分数形式吗?
能化为分数形式吗?
探求:步骤①设![]() ,步骤②
,步骤②![]() ,
,
步骤③![]() ,则
,则![]() ,
,
步骤④![]() ,解得:
,解得:![]() .
.
根据你对这段文字的理解,回答下列问题:
(1)步骤①到步骤②的依据是什么;
(2)仿照上述探求过程,请你尝试把![]() 化为分数形式:
化为分数形式:
(3)请你将![]() 化为分数形式,并说明理由.
化为分数形式,并说明理由.
参考答案:
【答案】(1) 等式的基本性质2: 等式两边都乘以或除以同一个数(除数不能为0),所得的等式仍然成立;(2)![]() ;(3)
;(3)![]() ,理由见详解.
,理由见详解.
【解析】
分析: (1) 利用等式的基本性质得出答案;
(2) 利用已知设x=![]() , 进而得出100x=37+x,求出即可;
, 进而得出100x=37+x,求出即可;
(3) 设y=![]() ,可得10y=0.
,可得10y=0.![]() =0.8+
=0.8+![]() =0.8+y,可得y的值,由
=0.8+y,可得y的值,由![]() =0.3+
=0.3+![]() 可得答案.
可得答案.
解: (1) 等式的基本性质2: 等式两边都乘以或除以同一个数(除数不能为0),所得的等式仍然成立.
(2)设x=![]()
100x=100![]()
![]()
100x=37.![]() ,100x=37+
,100x=37+![]()
100x=37+x,
99x=37,
解得:x=![]() ;
;
(3)同理设y=![]() ,
,
10y=0.![]() =0.8+
=0.8+![]() =0.8+y
=0.8+y
解得:y=![]() ,
,
故![]() =0.3+
=0.3+![]() =
=![]() =
=![]()
故答案:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式
 ,并把解在数轴上表示出来.
,并把解在数轴上表示出来. 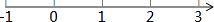
-
科目: 来源: 题型:
查看答案和解析>>【题目】有足够多的长方形和正方形卡片,如下图:
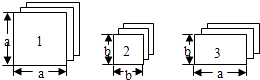
(1)如果选取1号、2号、3号卡片分别为1张、2张、3张,可拼成一个长方形(不重叠无缝隙),请画出这个长方形的草图,并运用拼图前后面积之间的关系说明这个长方形的代数意义.
这个长方形的代数意义是 .
(2)小明想用类似方法解释多项式乘法(a+3b)(2a+b)=2a2+7ab+3b2 , 那么需用2号卡片张,3号卡片张. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校初一年级两个班的学生要到航天科普教育基地进行社会大课堂活动,两班学生共104人,其中初一(1)班有40多人,不足50人,教育基地门票价格如下:
购票张数
1~50张
51~100张
100张以上
每张票的价格
12元
10元
8元
原计划两班都以班为单位购票,则一共应付1240元,请回答下列问题:
(1)初一(1)班有多少人?
(2)你作为组织者如何购票最省钱?比原计划省多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量? 操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验,摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中,再继续.
活动结果:摸球实验活动一共做了50次,统计结果如下表:球的颜色
无记号
有记号
红色
黄色
红色
黄色
摸到的次数
18
28
2
2
推测计算:由上述的摸球实验可推算:
(1)盒中红球、黄球各占总球数的百分比分别是多少?
(2)盒中有红球多少个? -
科目: 来源: 题型:
查看答案和解析>>【题目】在(1)
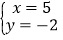 (2)
(2) 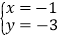 (3)
(3) 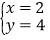 (4)
(4) 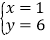 中,________是方程7x-3y=2的解;________是方程2x+y=8的解;________是方程组
中,________是方程7x-3y=2的解;________是方程2x+y=8的解;________是方程组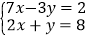 的解.(填序号)
的解.(填序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】某花圃用花盆培育某种花苗,经过试验发现每盆的盈利与每盆的株数构成一定的关系,每盆植入3株时,平均单株盈利3元,以同样的栽培条件,若每盆增加1株,平均单株盈利就减少0.5元,要使每盆的盈利达到10元,每盆应该植多少株? 小明的解法如下:
解:设每盆花苗增加x株,则每盆花苗有(x+3)株,平均单株盈利为(3﹣0.5x)元,
由题意得(x+3)(3﹣0.5x)=10,
化简,整理得:x2﹣3x+2=0
解这个方程,得:x1=1,x2=2,
答:要使每盆的盈利达到10元,每盆应该植入4株或5株.
(1)本题涉及的主要数量有每盆花苗株数,平均单株盈利,每盆花苗的盈利等,请写出两个不同的等量关系: .
(2)请用一种与小明不相同的方法求解上述问题.
相关试题

