【题目】如图,在ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
(1)求证:四边形BECD是平行四边形;
(2)若∠A=50°,则当∠BOD= ______ °时,四边形BECD是矩形.

参考答案:
【答案】(1)证明见解析;(2)100
【解析】(1)证明:∵四边形ABCD为平行四边形,∴AB∥DC,AB=CD,∴∠OEB=∠ODC,又∵O为BC的中点,∴BO=CO,在△BOE和△COD中,∵∠OEB=∠ODC,∠BOE=∠COD,BO=CO,∴△BOE≌△COD(AAS);
∴OE=OD,∴四边形BECD是平行四边形;
(2)解:若∠A=50°,则当∠BOD=100°时,四边形BECD是矩形.理由如下:
∵四边形ABCD是平行四边形,∴∠BCD=∠A=50°,∵∠BOD=∠BCD+∠ODC,∴∠ODC=100°﹣50°=50°=∠BCD,∴OC=OD,∵BO=CO,OD=OE,∴DE=BC,∵四边形BECD是平行四边形,∴四边形BECD是矩形;
故答案为:100.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一架梯子AC长2.5米,斜靠在一面墙上,梯子底端离墙0.7米.
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了0.4米到A′,那么梯子的底端在水平方向滑动了几米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
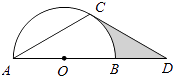
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根x1、x2 .
(1)求实数k的取值范围.
(2)若方程两实根x1、x2满足x1+x2=﹣x1x2 , 求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD、EF都经过点O,且AB⊥CD,OG平分∠BOE,如果∠EOG=
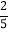 ∠AOE,求∠EOG,∠DOF和∠AOE.
∠AOE,求∠EOG,∠DOF和∠AOE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了做好大课间活动,计划用400元购买10件体育用品,备选体育用品及单价如下表(单位:元)
备选体育用品
篮球
排球
羽毛球拍
单价(元)
50
40
25
(1)若400元全部用来购买篮球和羽毛球拍共10件,问篮球和羽毛球拍各购买多少件?
(2)若400元全部用来购买篮球、排球和羽毛球拍三种共10件,能实现吗?(若能实现直接写出一种答案即可,若不能请说明理由.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC在正方形网格中,若A(0,3),按要求回答下列问题
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出B和C的坐标;
(3)计算△ABC的面积.

相关试题

