【题目】如图,在平行四边形ABCD中,已知点E在AB上,点F在CD上,且AE=CF.
求证:DE=BF.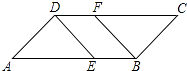
参考答案:
【答案】证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∵AE=CF.
∴BE=FD,BE∥FD,
∴四边形EBFD是平行四边形,
∴DE=BF
【解析】方法一:根据平行四边形的性质得出AB平行且等于CD,由AE=CF得出BE=FD,BE∥FD,即可证得四边形EBFD是平行四边形,根据平行四边形的性质即可证得结论。
方法二:由已知平行四边形得出对角相等,对边相等,再证明△ADE≌△CBF,即可求得DE=CF.
【考点精析】本题主要考查了平行四边形的判定与性质的相关知识点,需要掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,∠ADC的平分线交AB于点E,∠ABC的平分线交CD于点F,求证:四边形EBFD是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一慢车和一快车沿相同路线从A地到B地,所行的路程与时间的图象如图所示,试根据图象,回答下列问题:
(1)慢车比快车早出发______小时,快车追上慢车时行驶了_____千米,快车比慢车早______小时到达B地;
(2)求慢车、快车的速度;
(3)快车追上慢车需几个小时?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形
 中,在
中,在 边上取两点
边上取两点 、
、 ,使
,使 .若
.若 ,
, ,
, , 则以
, 则以 ,
, ,
, 为边长的三角形的形状为( )
为边长的三角形的形状为( )
A.锐角三角形B.直角三角形C.钝角三角形D.随
 ,
, ,
, 的值而定
的值而定 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)图1阴影面积可表示为_______,图2阴影面积可表示为_____.
请利用图形面积的不同表示方法,写出一个关于
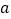 、
、 的恒等式_______.
的恒等式_______.
(2)如图所示的长方形或正方形三类卡片各有若干张,请你用这些卡片,拼成一个长方形或正方形图形。验证公式(a+b)2=a2+2ab+b2.

(3)图
 是一个长为2m、宽为2m的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图
是一个长为2m、宽为2m的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图 的形状拼成一个正方形。
的形状拼成一个正方形。
请用两种不同的方法求图
 中阴影部分的面积:
中阴影部分的面积:方法1:___________________;
方法2:__________________;
观察图
 写出下列三个代数式之间的等量关系:
写出下列三个代数式之间的等量关系: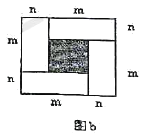
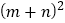 ,
,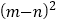 ,
,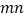
_____________________________;
(4)根据(3)题中的等量关系,解决如下问题:
若
 ,
,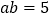 ,则
,则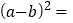 ________.
________. -
科目: 来源: 题型:
查看答案和解析>>【题目】观察一列数:1、2、4、8、16、32、…,发现从第二项开始,每一项与前一项的比值都是同一个常数,这个常数是_______;根据此规律,如果
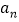 (
(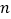 为正整数)表示这个数列的第
为正整数)表示这个数列的第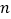 项,如果
项,如果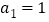 ,
,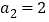 ,那么
,那么 _____,…,
_____,…,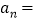 _______;
_______;如果欲求
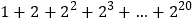 的值,
的值,可令
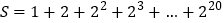 …………①
…………①将①式两边同乘以2,得
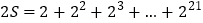 ……………②
……………②由②减去①式,得
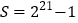 .
.(2)类比可得:
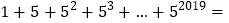 __________.
__________.(3)用由特殊到一般的方法知:若数列
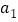 、
、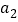 、
、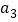 、…、
、…、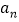 ,从第二项开始每一项与前一项之比的常数为
,从第二项开始每一项与前一项之比的常数为 ,那么
,那么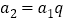 ,
, ____,…,
____,…,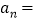 ______ (用含
______ (用含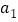 ,
,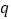 ,
,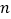 的代数式表示).
的代数式表示).用含
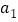 ,
,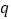 ,
,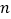 的代数式表示
的代数式表示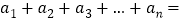 _________.
_________.(4)一质点从距离原点一个单位的A点向原点方向跳动,第一次跳到OA中点
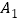 处,第二次从
处,第二次从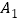 跳到
跳到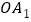 的中点
的中点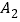 处,第三次从
处,第三次从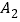 跳到
跳到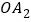 的中点
的中点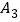 处,…,如此不断跳下去,则第50次跳动后,该质点跳动的距离是多少?
处,…,如此不断跳下去,则第50次跳动后,该质点跳动的距离是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰
 中,
中, ,
, , 底角为
, 底角为 ,动点
,动点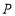 从点
从点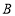 向点
向点 运动,当
运动,当 是直角三角形是
是直角三角形是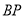 长为( )
长为( )A.4B.2或3C.3或4D.3
相关试题

