【题目】如图,在ABCD中,∠ADC的平分线交AB于点E,∠ABC的平分线交CD于点F,求证:四边形EBFD是平行四边形. 
参考答案:
【答案】解:∵四边形ABCD是平行四边形, ∴AD=CB,∠A=∠C,∠ADC=∠ABC.
又∵∠ADF= ![]() ∠ADC,∠CBE=
∠ADC,∠CBE= ![]() ∠ABC,
∠ABC,
∴∠ADF=∠CBE.
∴△ADF≌△CBE.
∴AF=CE.
∴AB﹣AF=CD﹣CE即DE=FB.
又∵DE∥BF,
∴四边形EBFD是平行四边形
【解析】由在ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F,易证得∠AFD=∠CDE=∠ABE,继而证得DF∥BE,则可证得四边形DFBE是平行四边形,
【考点精析】利用平行四边形的判定与性质对题目进行判断即可得到答案,需要熟知若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式x-3>1的解集是( )
A. x>2 B. x>4 C. x>-2 D. x>-4
-
科目: 来源: 题型:
查看答案和解析>>【题目】把47155精确到百位可表示为
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下列证明过程,求证:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
已知:________
求证:________ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ACB与△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE上,求证:AE2+AD2=2AC2 . (提示:连接BD)
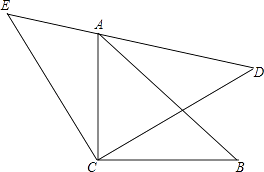
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
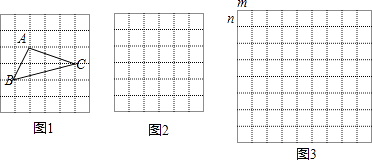
(1)在△ABC中,AB、BC、AC三边的长分别为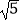 、
、 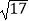 、
、 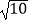 ,求这个三角形的面积. 如图1,某同学在解答这道题时,先建立一个每个小正方形的边长都是1的网格,再在网格中画出边长符合要求的格点三角形ABC(即△ABC三个顶点都在小正方形的顶点处),这样不需要求△ABC的高,而借用网格就能就算出它的面积.
,求这个三角形的面积. 如图1,某同学在解答这道题时,先建立一个每个小正方形的边长都是1的网格,再在网格中画出边长符合要求的格点三角形ABC(即△ABC三个顶点都在小正方形的顶点处),这样不需要求△ABC的高,而借用网格就能就算出它的面积.
请你将△ABC的面积直接填写在横线上 .
(2)思维拓展: 已知△ABC三边的长分别为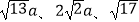 a(a>0),求这个三角形的面积.
a(a>0),求这个三角形的面积.
我们把上述求△ABC面积的方法叫做构图法.如图2,网格中每个小正方形的边长都是a,请在网格中画出相应的△ABC,并求出它的面积.
(3)类比创新: 若△ABC三边的长分别为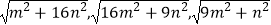 (m>0,n>0,且m≠n),求出这个三角形的面积.
(m>0,n>0,且m≠n),求出这个三角形的面积.
如图3,网格中每个小长方形长、宽都是m,n,请在网格中画出相应的△ABC,用网格计算这个三角形的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列叙述,其中不正确的是( )
A. 过一点有且只有一条直线与已知直线平行 B. 同角(或等角)的余角相等
C. 两点确定一条直线 D. 两点之间的所有连线中,线段最短
相关试题

