【题目】图1、图2中,点C为线段AB上一点,△ACM与△CBN都是等边三角形.
(1) 如图1,线段AN与线段BM是否相等?证明你的结论;
(2) 如图2,AN与MC交于点E,BM与CN交于点F,探究△CEF的形状,并证明你的结论.

图1 图2
参考答案:
【答案】(1)相等,证明见解析;(2)△CEF的形状是等边三角形.
【解析】
(1)等边三角形的性质可以得出△ACN、△MCB两边及夹角分别对应相等,;两个三角形全等,得出线段AN=BM;(2)平角的定义得出∠MCN=60°,通过证明△ACE≌△MCF,得出CE=CF,根据等边三角形的判定得出△CEF的形状.
(1)∵△ACM与△CBN都是等边三角形,
∴AC=MC,CN=CB,∠ACM=∠BCN=60°.
∴∠MCN=60°,∠ACN=∠MCB,
在△ACN和△MCB中,
AC=MC, ∠ACN=∠MCB,CN=CB,
∴△ACN≌△MCB(SAS),∴AN=BM.
(2)∵∠ACM=60°,∠MCN=60°,∴∠ACM=∠MCN,
∵△ACN≌△MCB,
∴∠CAE=∠CMB.
在△ACE和△MCF中,
∠CAE=∠CMF,AC=MC, ∠ACE=∠MCF,
∴△ACE≌△MCF(ASA),
∴CE=CF,
∴△CEF的形状是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】固始县教体局举办”我的中国梦“为主题的知识竞赛,甲、乙两所学校参赛人数相等.比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并依据统计数据绘制了如下不完整的统计图表.
乙校成绩统计表分数(分)
70分
80分
90分
100分
人数(人)
7
1
8
(1)在图①中,“80分”所在扇形的圆心角度数为 .
(2)请你将图②补充完整.
(3)通过计算,说明哪所学校的学生成绩较整齐. -
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)将一张长方形纸条ABCD按如图所示折叠,若折叠角∠FEC=64°.
(1)求∠1的度数;
(2)求证:△EFG是等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装公司招工广告承诺:熟练工人每月工资至少3000元.每天工作8小时,一个月工作25天.月工资底薪800元,另加计件工资.加工1件A型服装计酬16元,加工1件B型服装计酬12元.在工作中发现一名熟练工加工1件A型服装和2件B型服装需4小时,加工3件A型服装和1件B型服装需7小时.(工人月工资=底薪+计件工资)
(1)一名熟练工加工1件A型服装和1件B型服装各需要多少小时?
(2)一段时间后,公司规定:“每名工人每月必须加工A,B两种型号的服装,且加工A型服装数量不少于B型服装的一半”.设一名熟练工人每月加工A型服装a件,工资总额为W元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺? -
科目: 来源: 题型:
查看答案和解析>>【题目】李明到离家2.1千米的学校参加八年级联欢会,到学校时发现演出道具还放在家中,此时距联欢会开始还有42分钟,于是他立即步行(匀速)回家,在家拿道具用了1分钟,然后立即骑自行车(匀速)返回学校,已知李明骑自行车到学校比他从学校步行到家用时少20分钟,且骑自行车的速度是步行速度的3倍。
(1)李明步行的速度(单位:米/分)是多少?
(2)李明能否在联欢会开始前赶到学校?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a是最大的负整数,b是5的相反数,c=|2|,且a、b、c分别是点A. B.C在数轴上对应的数.
(1)求a、b、c的值,并在数轴上标出点A. B. C.
(2)若动点P从点A出发沿数轴正方向运动,动点Q同时从点B出发也沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒1个单位长度,求运动几秒后,点Q可以追上点P?
(3)在数轴上找一点M,使点M到A. B.C三点的距离之和等于12,请直接写出所有点M对应的数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】问题探究:
(1)已知:如图1,在正方形ABCD中,点E、H分别在BC、AB上,若AE⊥DH于点O,求证AE=DH;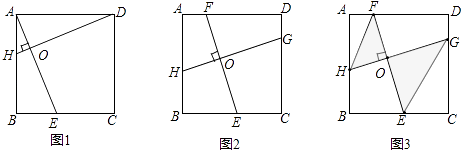
类比探究:
(2)如图2,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上,若EF⊥HG于点O,探究线段EF与HG的数量关系,并说明理由;
拓展应用:
(3)已知,如图3,在(2)问条件下,若BC=4,E为BC的中点,AF= AD,求HG的长
AD,求HG的长
相关试题

