【题目】如图,已知在矩形![]() 中,
中,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 的中点,
的中点,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 的中点.
的中点.

(1)求证:![]() ;
;
(2)判断四边形![]() 是什么特殊四边形,并证明你的结论;
是什么特殊四边形,并证明你的结论;
(3)当![]() ________时,四边形
________时,四边形![]() 是正方形(只写结论,不需证明)
是正方形(只写结论,不需证明)
参考答案:
【答案】(1)详见解析;(2)四边形![]() 是菱形,详见解析;(3)
是菱形,详见解析;(3)![]()
【解析】
(1)求出AB=DC,∠A=∠D=90°,AM=DM,根据全等三角形的判定定理推出即可;
(2)根据三角形中位线定理求出NE∥MF,NE=MF,得出平行四边形,求出BM=CM,推出ME=MF,根据菱形的判定推出即可;
(3)求出∠EMF=90°,根据正方形的判定推出即可.
(1)证明:∵四边形ABCD是矩形,
∴AB=DC,∠A=∠D=90°,
∵M为AD中点,
∴AM=DM,
在△ABM和△DCM,
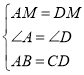 ,
,
∴△ABM≌△DCM(SAS);
(2)答:四边形MENF是菱形.
证明:∵N、E、F分别是BC、BM、CM的中点,
∴NE∥CM,NE=![]() CM,MF=
CM,MF=![]() CM,
CM,
∴NE=FM,NE∥FM,
∴四边形MENF是平行四边形,
由(1)知△ABM≌△DCM,
∴BM=CM,
∵E、F分别是BM、CM的中点,
∴ME=MF,
∴平行四边形MENF是菱形;
(3)解:当四边形MENF是正方形时,则∠EMF=90°,
∵△ABM≌△DCM,
∴∠AMB=∠DMC=45°,
∴△ABM、△DCM为等腰直角三角形,
∴AM=DM=AB,
∴AD=2AB,
当AB:AD=1:2时,四边形MENF是正方形.
故答案为:1:2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.

(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=8,求四边形OCED的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小叶与小高欲测量公园内某棵树DE的高度.他们在这棵树正前方的一座楼亭前的台阶上的点A处测得这棵树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得这棵树顶端D的仰角为60°.已知点A的高度AB为3 m,台阶AC的坡度为1∶
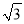 ,且B,C,E三点在同一条直线上,那么这棵树DE的高度为( )
,且B,C,E三点在同一条直线上,那么这棵树DE的高度为( )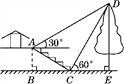
A. 6 m B. 7 m C. 8 m D. 9 m
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的高,tanB=cos∠DAC.
(1)求证:AC=BD;
(2)若sin C=
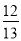 ,BC=12,求△ABC的面积.
,BC=12,求△ABC的面积.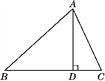
-
科目: 来源: 题型:
查看答案和解析>>【题目】电脑公司销售甲、乙两种型号的计算机,甲型标价 5500 元/台,乙型标价 5000 元/台.
(1)若甲种计算机有 60 台,两种计算机全部销售完以后,销售总额超过 55 万元,这批计算最少有多少台?
(2)电脑公司开展优惠活动,甲型降价 100 元/台,乙型降价 200 元/台,按降价后价格将两种计算机全部售出后的销售总额比按标价全部售出的销售总额减少了 2 万元,已知甲种计算机的台数多于乙种的台数,求乙种计算机最多有多少台?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到0.1米)

-
科目: 来源: 题型:
查看答案和解析>>【题目】探索:如图1,在
 中,
中, ,
, .求证:
.求证: ;
;发现:直角三角形中,如果有一个锐角等于
 ,那么这个角所对的直角边等于斜边的_______.
,那么这个角所对的直角边等于斜边的_______.应用:如图2,在
 中,
中, ,
, ,
, ,点
,点 从点
从点 出发沿
出发沿 方向以
方向以 秒的速度向点
秒的速度向点 匀速运动,同时点
匀速运动,同时点 从点
从点 出发沿
出发沿 方向以
方向以 秒的速度向点
秒的速度向点 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点
匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点 运动的时间是
运动的时间是 秒(
秒( ).过点
).过点 作
作 于点
于点 ,连接
,连接 ,
, .
.
(1)四边形
 能够成为菱形吗?如果能,求出相应的
能够成为菱形吗?如果能,求出相应的 值;如果不能,请说明理由;
值;如果不能,请说明理由;(2)当
 为何值时,
为何值时, 为直角三角形?请说明理由.
为直角三角形?请说明理由.
相关试题

