搜索
【题目】如图，边长为a的正方形木块在水平地面上沿直线滚动一周（没有滑动），则它的中心点O所经过的路径长为（ ）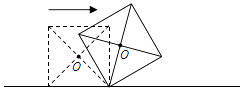 
A.4a
B.2 
πa
C. πa
D. a
参考答案：
【答案】C
【解析】解：如图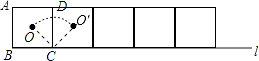 
∵四边形ABCD为正方形，且边长为a，
∴OC= 
a，∠OCO′=90°，
∵边长为a的正方形ABCD沿直线l向右做无滑动地翻滚，当正方形翻滚一周时，需要翻滚四次，
而每次正方形的中心O所经过的路径长为弧OO′（以C为圆心，OC为半径），
∴弧OO′的长= 
= 
aπ，
∴当正方形翻滚一周时，正方形的中心O所经过的路径长=4× aπ= 
aπ．
故选C．
根据正方形的性质易得OC= a，∠OCO′=90°，又边长为a的正方形ABCD沿直线l向右做无滑动地翻滚，当正方形翻滚一周时，需要翻滚四次，而每次正方形的中心O所经过的路径长为弧OO′（以C为圆心，OC为半径），然后根据弧长公式计算出弧OO′的长，再乘以4即可．
-
科目： 来源： 题型：
查看答案和解析>>【题目】把正整数1，2，3，4，2016排列成如图所示的形式.
（1）用一个矩形随意框住4个数，把其中最小的数记为
,另三个数用含式子表示出来，当被框住的4个数之和等于418时，值是多少？（2）被框住的4个数之和能否等于724？如果能，请求出此时x值；如果不能，请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】小李到某城市行政中心大楼办事，假定乘电梯向上一楼记为+1，向下一楼记为–1．
小李从1楼出发，电梯上下楼层依次记录如下（单位：层）： +5，–3，+10，–8，+12，–6，–10．
（1）请你通过计算说明小李最后是否回到出发点1楼；
（2）该中心大楼每层高2.8m，电梯每上或下1m需要耗电0.1度．根据小李现在所处的位置，请你算一算，当他办事时电梯需要耗电多少度？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB＝BC，BE⊥AC于点E，AD⊥BC于点D，
∠BAD＝45°，AD与BE交于点F，连接CF.
（1）求证：BF＝2AE；
（2）若CD＝
，求AD的长. -
科目： 来源： 题型：
查看答案和解析>>【题目】勾股定理是一条古老的数学定理，它有很多种证明方法，我国汉代数学家赵爽根据弦图，利用面积法进行证明，著名数学家华罗庚曾提出把“数形关系”（勾股定理）带到其他星球，作为地球人与其他星球“人”进行第一次“谈话”的语言．
[定理表述]
请你写出勾股定理内容（用文字语言表述）：
[尝试证明]
以图1中的直角三角形为基础，可以构造出以a、b为底，以（a+b）为高的直角梯形（如图2），请你利用图2，证明勾股定理．
-
科目： 来源： 题型：
查看答案和解析>>【题目】现在，苏宁商场进行促销活动，出售一种优惠购物卡（注：此卡只作为购物优惠凭证不能顶替货款），花300元买这种卡后，凭卡可在这家商场按标价的8折购物.
（1）顾客购买多少元金额的商品时，买卡与不买卡花钱相等？在什么情况下购物合算？
（2）小张要买一台标价为3500元的冰箱，如何购买合算？小张能节省多少元钱？
（3）小张按合算的方案，把这台冰箱买下，如果商场还能盈利25％，这台冰箱的进价是多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，CE⊥AB于点E，DF⊥AB于点F，CE平分∠ACB，DF平分∠BDE，
求证：AC∥ED.
证明：∵CE⊥AB于E，DF⊥AB于F（已知）
∴DF∥ （垂直于同一条直线的两直线平行）
∴∠BDF=∠ （ ）
∠FDE=∠ （两直线平行，内错角相等）
∵CE平分∠ACB，DF平分∠BDE（已知）
∴∠ACE=∠ECB，∠EDF=∠BDF（角平分线的定义）
∴∠ACE=∠ （等量代换）
∴AC∥ED（ ）.
相关试题
