【题目】如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒,当t为时,△ACP是等腰三角形. 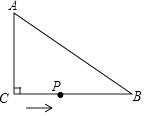
参考答案:
【答案】3或6或6.5或5.4
【解析】解:∵AC=6,BC=8, ∴由勾股定理可知:AB=10,
当点P在CB上运动时,
由于∠ACP=90°,
∴只能有AC=CP,如图1,
∴CP=6,
∴t= ![]() =3,
=3,
当点P在AB上运动时,①AC=AP时,如图2,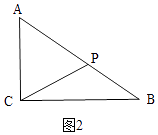
∴AP=6,PB=AB﹣CP=10﹣6=4,
∴t= ![]() =6,②当AP=CP时,如图3,
=6,②当AP=CP时,如图3,
此时点P在线段AC的垂直平分线上,
过点P作PD⊥AC于点D,
∴CD= ![]() AC=3,PD是△ACB的中位线,
AC=3,PD是△ACB的中位线,
∴PD= ![]() BC=4,
BC=4,
∴由勾股定理可知:AP=5,
∴PB=5,
∴t= ![]() =6.5;③AC=PC时,如图4,
=6.5;③AC=PC时,如图4,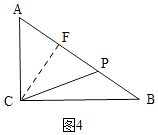
过点C作CF⊥AB于点F,
∴cos∠A= ![]() =
= ![]() ,
,
∴AF=3.6,
∴AP=2AF=7.2,
∴PB=10﹣7.2=2.8,
∴t= ![]() =5.4;
=5.4;
综上所述,当t为3或6或6.5或5.4时,△ACP是等腰三角形.
故答案为:3或6或6.5或5.4.
由于没有说明哪一条边是腰,故需要分情况讨论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班组织了一次读书活动,统计了16名同学在一周内的读书时间,他们一周内的读书时间累计如表,则这16名同学一周内累计读书时间的中位数是 .
一周内累计的读书时间(小时)
5
8
10
14
人数(个)
1
7
5
3
-
科目: 来源: 题型:
查看答案和解析>>【题目】从﹣3,﹣2,﹣1,0,1,3,4这七个数中随机抽取一个数记为a,a的值既是不等式组
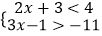 的解,又在函数y=
的解,又在函数y= 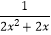 的自变量取值范围内的概率是 .
的自变量取值范围内的概率是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】对于实数
 、
、 我们定义一种新运算
我们定义一种新运算 (其中
(其中 、
、 均为非零常数).等式右边是通常的四则运算.由这种运算得到的数我们称之为线性数,记为
均为非零常数).等式右边是通常的四则运算.由这种运算得到的数我们称之为线性数,记为 ,其中
,其中 、
、 叫做线性数的一个数对.若实数
叫做线性数的一个数对.若实数 、
、 都取正整数,我们称这样的线性数为正格线性数,这时的
都取正整数,我们称这样的线性数为正格线性数,这时的 、
、 叫做正格线性数的正格数对.
叫做正格线性数的正格数对.(1)若
 ,则
,则
 .
.(2)已知
 ,若正格线性数
,若正格线性数 ,求满足不等式组
,求满足不等式组 的所有
的所有 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】威丽商场销售A、B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元?
(2)由于需求量大,A、B两种商品很快售完,威丽商场决定再一次购进A、B两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么威丽商场至少需购进多少件A种商品?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(2,0),B(2,4),定义:若平面内点P关于直线AB的对称点Q在图形M内或图形的边界上,则称点P是图形M关于直线AB的“反称点”.
(1)已知C(5,0),D(5,3)
①点M1(0,3),M2(-0. 5,2),M3(-2,1),则是△ACD关于直线AB的“反称点”的是________:
②若直线y=2x+m上存在△ACD关于直线AB的“反称点”,求m的取值范围;
(2)已知点E(1,0),F(5,0),
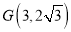 ,点P(x,y)在直线y=x+1上,且点P是△EFG的反称点,求点P横坐标的取值范围.
,点P(x,y)在直线y=x+1上,且点P是△EFG的反称点,求点P横坐标的取值范围. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=1,则FM的长为 .

相关试题

