【题目】已知A(2,0),B(2,4),定义:若平面内点P关于直线AB的对称点Q在图形M内或图形的边界上,则称点P是图形M关于直线AB的“反称点”.
(1)已知C(5,0),D(5,3)
①点M1(0,3),M2(-0. 5,2),M3(-2,1),则是△ACD关于直线AB的“反称点”的是________:
②若直线y=2x+m上存在△ACD关于直线AB的“反称点”,求m的取值范围;
(2)已知点E(1,0),F(5,0), ![]() ,点P(x,y)在直线y=x+1上,且点P是△EFG的反称点,求点P横坐标的取值范围.
,点P(x,y)在直线y=x+1上,且点P是△EFG的反称点,求点P横坐标的取值范围.
参考答案:
【答案】(1)①M2;②-4≤m≤5(2)![]()
【解析】试题分析:根据“反称点”的定义解答即可.
试题解析:解:(1)①设直线AD的解析式为y=kx+b,则: ![]() ,解得:
,解得: ![]() ,∴直线AD为:y=x-2.点M1(0,3)关于直线AB的对称点为Q(4,3),当x=4时,y=x-2=2.∵2<3,∴Q在△ACD外,∴M1不是△ACD关于直线AB的“反称点”;
,∴直线AD为:y=x-2.点M1(0,3)关于直线AB的对称点为Q(4,3),当x=4时,y=x-2=2.∵2<3,∴Q在△ACD外,∴M1不是△ACD关于直线AB的“反称点”;
点M2(-0.5,2)关于直线AB的对称点为Q(4.5,2),当x=4.5时,y=x-2=2.5.∵2.5>2,∴Q在△ACD内,∴M2是△ACD关于直线AB的“反称点”;
点M3(-2,1)于直线AB的对称点为Q(6,1).∵6>5,∴Q在△ACD外,∴M3不是△ACD关于直线AB的“反称点”;
②设M(a,2a+m)在直线y=2x+m上,M关于直线AB的对称点为 Q(4-a,2a+m),则2≤4-a≤5,0≤2a+m≤2-a,解得:-1≤a≤2,-4≤m≤5;
(2)易求直线EF的解析式为![]() .点P(a,a+1)在直线y=x+1上,P关于直线AB的对称点为Q(4-a,a+1),则1≤4-a≤5,0≤a+1≤
.点P(a,a+1)在直线y=x+1上,P关于直线AB的对称点为Q(4-a,a+1),则1≤4-a≤5,0≤a+1≤![]() ,解得:-1≤a≤
,解得:-1≤a≤![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于实数
 、
、 我们定义一种新运算
我们定义一种新运算 (其中
(其中 、
、 均为非零常数).等式右边是通常的四则运算.由这种运算得到的数我们称之为线性数,记为
均为非零常数).等式右边是通常的四则运算.由这种运算得到的数我们称之为线性数,记为 ,其中
,其中 、
、 叫做线性数的一个数对.若实数
叫做线性数的一个数对.若实数 、
、 都取正整数,我们称这样的线性数为正格线性数,这时的
都取正整数,我们称这样的线性数为正格线性数,这时的 、
、 叫做正格线性数的正格数对.
叫做正格线性数的正格数对.(1)若
 ,则
,则
 .
.(2)已知
 ,若正格线性数
,若正格线性数 ,求满足不等式组
,求满足不等式组 的所有
的所有 的值.
的值. -
科目: 来源: 题型:
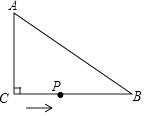
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒,当t为时,△ACP是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】威丽商场销售A、B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元?
(2)由于需求量大,A、B两种商品很快售完,威丽商场决定再一次购进A、B两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么威丽商场至少需购进多少件A种商品?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=1,则FM的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2+ax+a﹣2=0.
(1)若该方程的一个根为2,求a的值及该方程的另一根.
(2)求证:不论a取何实数,该方程都有两个不相等的实数根. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形的顶点A(1,1)、B(3,1),规定把等边△ABC“先沿x轴翻折,再向左平移1个单位”为一次変换,如果这样连续经过2016次变换后,等边△ABC的顶点C的坐标为________________________.

相关试题

