【题目】为响应绿色出行号召,越来越多市民选择租用共享单车出行,已知某共享单车公司为市民提供了手机支付和会员卡支付两种支付方式,如图描述了两种方式应支付金额y(元)与骑行时间x(时)之间的函数关系,根据图象回答下列问题:
(1)求手机支付金额y(元)与骑行时间x(时)的函数关系式;
(2)李老师经常骑行共享单车,请根据不同的骑行时间帮他确定选择哪种支付方式比较合算.

参考答案:
【答案】(1)手机支付金额y(元)与骑行时间x(时)的函数关系式是y=![]() ;
;
(2)当x=2时,李老师选择两种支付方式一样;当x>2时,会员卡支付比较合算;当0<x<2时,李老师选择手机支付比较合算.
【解析】试题分析:
(1)由图可知,“手机支付”的函数图象过点(0.5,0)和点(1,0.5),由此即可由“待定系数法”求得对应的函数解析式;
(2)先用“待定系数法”求得“会员支付”的函数解析式,结合(1)中所得函数解析式组成方程组,即可求得两个函数图象的交点坐标,由交点坐标结合图象即可得到本题答案;
试题解析:
(1)由题意和图象可设:手机支付金额y(元)与骑行时间x(时)的函数解析式为: ![]() ,由图可得:
,由图可得: ![]() ,解得:
,解得: ![]() ,
,
∴手机支付金额y(元)与骑行时间x(时)的函数解析式为: ![]() ;
;
(2)由题意和图象可设会员支付y(元)与骑行时间x(时)的函数解析式为: ![]() ,
,
由图可得: ![]() ,
,
由![]() 可得:
可得: ![]() ,
,
∴图中两函数图象的交点坐标为(2,1.5),
又∵![]() ,
,
∴结合图象可得:
当![]() 时,李老师用“手机支付”更合算;
时,李老师用“手机支付”更合算;
当![]() 时,李老师选择两种支付分式花费一样多;
时,李老师选择两种支付分式花费一样多;
当![]() 时,李老师选择“会员支付”更合算.
时,李老师选择“会员支付”更合算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是ts.过点D作DF⊥BC于点F,连接DE、EF.

(1)用t的代数式表示:AE= ;DF= ;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小亮从家步行到公交车站台,等公交车去学校. 图中的折线表示小亮的行程s(km)与所花时间t(min)之间的函数关系. 下列说法错误的是

A. 他离家8km共用了30min B. 他等公交车时间为6min
C. 他步行的速度是100m/min D. 公交车的速度是350m/min
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置.

(1)旋转中心是点 , 旋转角度是度;
(2)若连结EF,则△AEF是三角形;并证明;
(3)若四边形AECF的面积为25,DE=2,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列两个等式:2﹣
 =2×
=2× +1,5﹣
+1,5﹣ =5×
=5× +1,给出定义如下:我们称使等式a﹣b=ab+1的成立的一对有理数a,b为“共生有理数对”,记为(a,b),如:数对(2,
+1,给出定义如下:我们称使等式a﹣b=ab+1的成立的一对有理数a,b为“共生有理数对”,记为(a,b),如:数对(2, ),(5,
),(5, ),都是“共生有理数对”.
),都是“共生有理数对”.(1)数对(﹣2,1),(3,
 )中是“共生有理数对”的是 ;
)中是“共生有理数对”的是 ;(2)若(m,n)是“共生有理数对”,则(﹣n,﹣m) “共生有理数对”(填“是”或“不是”);
(3)请再写出一对符合条件的“共生有理数对”为 ;(注意:不能与题目中已有的“共生有理数对”重复)
(4)若(a,3)是“共生有理数对”,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场同时购进甲、乙两种商品共
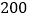 件,其进价和售价如右表,设其中甲种商品购进
件,其进价和售价如右表,设其中甲种商品购进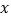 件.
件.(1)直接写出购进乙种商品的件数;(用含
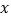 的代数式表示)
的代数式表示)(2)若设该商场售完这
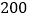 件商品的总利润为
件商品的总利润为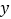 元.
元.①求
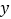 与
与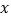 的函数关系式;
的函数关系式;②该商品计划最多投入
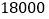 元用于购买这两种商品,则至少要购进多少件甲商品?若售完这些商品,则商场可获得的最大利润是多少元?
元用于购买这两种商品,则至少要购进多少件甲商品?若售完这些商品,则商场可获得的最大利润是多少元?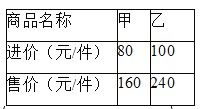
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,直线
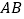 与
与 轴、
轴、 轴分别交于点
轴分别交于点 、点
、点 ,与双曲线
,与双曲线
 交于
交于 、
、 两点,分别过点
两点,分别过点 、点
、点 作
作 轴,
轴, 轴,垂足分别为点
轴,垂足分别为点 、点
、点 ,
,
(1)求线段
 的长;
的长;(2)若
 .
. ①求直线
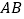 的解析式;
的解析式;②请你判断线段
 与线段
与线段 的大小关系,并说明理由.
的大小关系,并说明理由.
相关试题

