【题目】在RtΔABC中,∠B=90°,∠A=30°,DE垂直平分AC,交AC于点E,交AB于点D,连接CD,若BD=2,则AD的长是___.
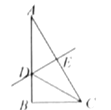
参考答案:
【答案】4
【解析】
首先根据题意DE垂直平分AC,可判断AD=CD,可得出△ADC是等腰三角形,∠A=∠ACD=30°,又因为在RtΔABC中,∠B=90°,∠A=30°,得出∠ACB=60°,∠BCD=30°,又由BD=2,根据三角函数值,得出sin∠BCD=![]() =
=![]() ,得出CD=4,进而得出AD=4.
,得出CD=4,进而得出AD=4.
解:∵DE垂直平分AC,
∴AD=CD,
∴△ADC是等腰三角形,∠A=∠ACD=30°
又∵在RtΔABC中,∠B=90°,∠A=30°,
∴∠ACB=60°,∠BCD=30°
又∵BD=2,
∴sin∠BCD=![]() =
=![]()
∴CD=4
∴AD=4.
故答案为4.
-
科目: 来源: 题型:
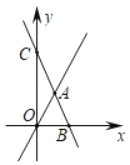
查看答案和解析>>【题目】已知直线l1:y=kx过点(1,2),与直线l2:y=﹣3x+b相交于点A,若l2与x轴交于点B(2,0),与y轴交于点C.
(1)分别求出直线11,l2的解析式;
(2)求△OAC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=120°,OP平分∠AOB,且OP=3,若点M,N分别在OA,OB上,ΔPMN为等边三角形,则满足上述条件的△PMN有中( )

A. 1个B. 2个C. 3个D. 3个以上
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于
 的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )
的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )
A. 2 B. 4 C. 6 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义一种新运算:a⊕b=
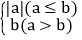
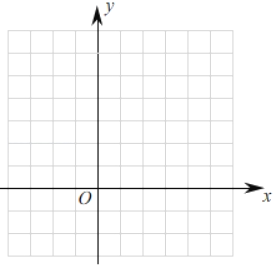
(1)请写出函数y=x⊕1的解析式,并在所给的平面直角坐标系中画出该函数图象;
(2)观察(1)中图象,探究得到y的最小值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿CE向上折叠,使点B落在AD边上的点F处.若AE=
 BE,则长AD与宽AB的比值是 .
BE,则长AD与宽AB的比值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,DE⊥AB,垂足为E.

(1)写出图中一对全等三角形和一对相似比不为1的相似三角形;
(2)选择(1)中一对加以证明.
相关试题

