【题目】(概念学习)
规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,如2÷2÷2,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)等.类比有理数的乘方,我们把2÷2÷2记作2③,读作“2的圈3次方”,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)记作(﹣3)④,读作“﹣3的圈4次方”,一般地,把 ![]() (a≠0)记作a,读作“a的圈n次方”.
(a≠0)记作a,读作“a的圈n次方”.
(1)(初步探究)
直接写出计算结果:2③=_______,(-![]() )⑤=_______;
)⑤=_______;
(2)(深入思考)
我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?
Ⅰ.试一试:仿照上面的算式,将下列运算结果直接写成幂的形式.
(﹣3)④=_______;5⑥=_______; (-![]() ) ⑩=_______.
) ⑩=_______.
Ⅱ. 想一想:将一个非零有理数a的圈n次方写成幂的形式等于_______;
Ⅲ. 算一算:
12÷(-![]() )④×(-2)⑤-(-
)④×(-2)⑤-(-![]() )⑥÷3.
)⑥÷3.
参考答案:
【答案】(1)【初步探究】
![]() ,-8;
,-8;
(2)【深入思考】
Ⅰ. ![]() ;
;![]() ;
;![]() ;
;
Ⅱ. ![]()
Ⅲ. ![]()
【解析】
(1)【初步探究】分别按公式进行计算即可;
(2)【深入思考】
Ⅰ.把除法化为乘法,第一个数不变,从第二个数开始依次变为倒数,由此分别得出结果;
Ⅱ.结果第一个数不变为a,第二个数及后面的数变为![]() ,则
,则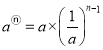
Ⅲ.将第二问的规律代入计算,注意运算顺序.
解:(1)【初步探究】
![]() ,
,
![]()
![]()
![]()
![]()
故答案为:![]() ,-8;
,-8;
(2)【深入思考】
Ⅰ. ![]() ;
;
![]() ;
;
![]()
故答案为:![]() ;
;![]() ;
;![]() ;
;
Ⅱ. ![]()
Ⅲ. ![]()
![]()
![]()
![]()
![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图一次函数y1=-x-2与y2=x-4的图象相交于点A.
(1)求点A的坐标;
(2)若一次函数y1=-x-2与y2=x-4的图象与x轴分别相交于点B、C,求△ABC的面积.
(3)结合图象,直接写出y1>y2时x的取值范围.

-
科目: 来源: 题型:
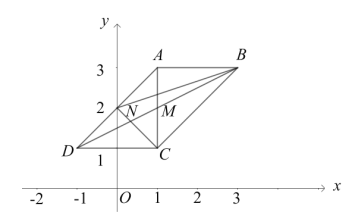
查看答案和解析>>【题目】如图,平行四边形ABCD的两个顶点坐标分别为A(1,3),B(3,3),对角线的交点为M(1,2),AD与y轴的交点为N.
(1)求C、D点的坐标;
(2)求证:△BCN的面积是平行四边形ABCD面积的一半;
(3)除了点N,坐标轴上是否存在点P,使△BCP的面积是平行四边形ABCD面积的一半,若存在,直接写出P点的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
 与y轴交于点
与y轴交于点 .
.(1)求抛物线的解析式;
(2)求抛物线与坐标轴的交点坐标;
(3)①当x取什么值时,
 ?
?  当x取什么值时,y的值随x的增大而减小?
当x取什么值时,y的值随x的增大而减小? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,AB=2,N为AB上一点,且AN=1,AD=
 ,∠BAC的平分线交BC于点D,M是AD上的动点,连接BM、MN,则BM+MN的最小值是( )
,∠BAC的平分线交BC于点D,M是AD上的动点,连接BM、MN,则BM+MN的最小值是( )
A.
 B. 2C. 1D. 3
B. 2C. 1D. 3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A是抛物线
 与x轴正半轴的交点,点B在抛物线上,其横坐标为2,直线AB与y轴交于点
与x轴正半轴的交点,点B在抛物线上,其横坐标为2,直线AB与y轴交于点 点M、P在线段AC上
点M、P在线段AC上 不含端点
不含端点 ,点Q在抛物线上,且MQ平行于x轴,PQ平行于y轴
,点Q在抛物线上,且MQ平行于x轴,PQ平行于y轴 设点P横坐标为m.
设点P横坐标为m.(1)求直线AB所对应的函数表达式.
(2)用含m的代数式表示线段PQ的长.
(3)以PQ、QM为邻边作矩形PQMN,求矩形PQMN的周长为9时m的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=mx+n与反比例函数y=
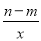 其中m、n为常数,且mn<0,则它们在同一坐标系中的图象可能是( )
其中m、n为常数,且mn<0,则它们在同一坐标系中的图象可能是( )A.
 B.
B.  C.
C.  D.
D. 
相关试题

