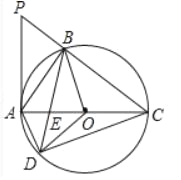
【题目】如图,在△ABC中,∠ABC=90°,⊙O是△ABC外接圆,点D是圆上一点,点D、B分别在AC两侧,且BD=BC,连接AD、BD、OD、CD,延长CB到点P,使∠APB=∠DCB.
(1)求证:AP为⊙O的切线;
(2)若⊙O的半径为1,当△OED是直角三角形时,求△ABC的面积;
(3)若△BOE、△DOE、△AED的面积分别为a、b、c,试探究a、b、c之间的等量关系式,并说明理由.

参考答案:
【答案】(1)证明见解析;(2)S△ABC=![]() 或
或![]() ;(3)b2=ac.
;(3)b2=ac.
【解析】试题分析:(1)欲证明PA是切线,只要证明PA⊥OA即可;
(2)分两种情形分别求解即可;
(3)只要证明AD∥OB,可得△AED∽△OEB,推出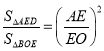 ,再推出
,再推出![]() 可得
可得![]() =(
=(![]() )2,b2=ac.
)2,b2=ac.
试题解析:
(1)证明:∵BD=BC,
∴∠BDC=∠BCD,
∵∠P=∠BCD,∠BAC=∠BDC,
∴∠P=∠BAC,
∵AC是直径,
∴∠ABC=∠ABP=90°,
∴∠P+∠BAP=90°,
∴∠BAP+∠BAC=90°,
∴∠OAP=90°,
∴OA⊥PA,
∴PA是⊙O的切线.
(2)解:①当∠OED=90°时,CB=CD=BD,△ABC是等边三角形,可得∠ACB=30°,
∵AC=2,
∴AB=1,BC=![]() ,
,
∴S△ABC=![]() .
.
②当∠DOE=90°时,易知∠AOB=45°,△ABC的AC边上的高=![]() ,
,
∴S△ABC=![]() .
.
(3)∵BD=BC,OD=OC,BO=BO,
∴△BOD≌△BOC,
∴∠OBD=∠OBC,
∵OB=OD=CO,
∴∠OBD=∠OBC=∠ODB=∠OCB,
∵∠ADB=∠OCB,
∴∠ADB=∠OBD,
∴AD∥OB,
∴△AED∽△OEB,
∴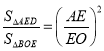 ,
,
∵![]() ,
,
∴![]() =(
=(![]() )2,
)2,
∴b2=ac.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB是平角,OD是∠AOC的角平分线,∠COE=∠BOE.

(1)若∠AOC= 50°,则∠DOE= °;
(2)当∠AOC的大小发生改变时,∠DOE的大小是否发生改变?为什么?
(3)图中与∠COD互补角的个数随∠AOC的度数变化而变化,直接写出与∠COD互补的角的个数及对应的∠AOC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是Rt△ABC斜边BC上的高.
(1)尺规作图:作∠C的平分线,交AB于点E,交AD于点F(不写作法,必须保留作图痕迹,标上应有的字母);
(2)在(1)的条件下,过F画BC的平行线交AC于点H,线段FH与线段CH的数量关系如何?请予以证明;
(3)在(2)的条件下,连结DEDH.求证:ED⊥HD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
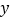 =
=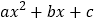 (
(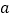 ≠0)与
≠0)与 轴交于AB两点,与
轴交于AB两点,与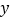 轴交于C点,其对称轴为
轴交于C点,其对称轴为 =1,且A(-1,0)C(0,2).
=1,且A(-1,0)C(0,2).(1)直接写出该抛物线的解析式;
(2)P是对称轴上一点,△PAC的周长存在最大值还是最小值?请求出取得最值(最大值或最小值)时点P的坐标;
(3)设对称轴与
 轴交于点H,点D为线段CH上的一动点(不与点CH重合).点P是(2)中所求的点.过点D作DE∥PC交
轴交于点H,点D为线段CH上的一动点(不与点CH重合).点P是(2)中所求的点.过点D作DE∥PC交 轴于点E.连接PDPE.若CD的长为
轴于点E.连接PDPE.若CD的长为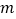 ,△PDE的面积为S,求S与
,△PDE的面积为S,求S与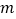 之间的函数关系式,试说明S是否存在最值,若存在,请求出最值,并写出S取得的最值及此时
之间的函数关系式,试说明S是否存在最值,若存在,请求出最值,并写出S取得的最值及此时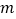 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数
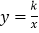 (x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是12,则k=( )
(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是12,则k=( )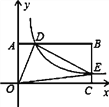
A. 6 B. 9 C.
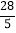 D.
D. 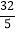
-
科目: 来源: 题型:
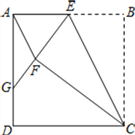
查看答案和解析>>【题目】如图,正方形ABCD中,点E为AB上一动点(不与A、B重合).将△EBC沿CE翻折至△EFC,延长EF交边AD于点G.
(1)连结AF,若 AF∥CE.证明:点E为AB的中点;
(2)证明:GF=GD;
(3)若AD=10,设EB=x,GD=y,求y与x的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下表,回答问题:
x
…
-2
-1
0
1
2
…
-2x+5
…
9
7
5
3
a
…
2x+8
…
4
6
8
10
b
…
(初步感知)
(1)a= ;b= ;
(归纳规律)
(2)随着x值的变化,两个代数式的值变化规律是什么?
(问题解决)
(3)比较-2x+5与2x+8的大小;
(4)请写出一个含x的代数式,要求x的值每增加1,代数式的值减小5,当x=0时,
代数式的值为-7.
相关试题

