【题目】如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点. 
(1)求此抛物线的解析式;
(2)直接写出点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE , 求P点坐标. 注:二次函数y=ax2+bx+c(a≠0)的顶点坐标为(﹣ ![]() ,
, ![]() )
)
参考答案:
【答案】
(1)解:由点A(﹣1,0)和点B(3,0)得 ![]() ,
,
解得: ![]() ,
,
∴抛物线的解析式为y=﹣x2+2x+3;
(2)解:令x=0,则y=3,
∴C(0,3),
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴D(1,4);
(3)解:设P(x,y)(x>0,y>0),
S△COE= ![]() ×1×3=
×1×3= ![]() ,S△ABP=
,S△ABP= ![]() ×4y=2y,
×4y=2y,
∵S△ABP=4S△COE,∴2y=4× ![]() ,
,
∴y=3,∴﹣x2+2x+3=3,
解得:x1=0(不合题意,舍去),x2=2,
∴P(2,3).
【解析】(1)将A、B的坐标代入抛物线的解析式中,即可求出待定系数b、c的值,进而可得到抛物线的对称轴方程;(2)令x=0,可得C点坐标,将函数解析式配方即得抛物线的顶点C的坐标;(3)设P(x,y)(x>0,y>0),根据题意列出方程即可求得y,即得D点坐标.
【考点精析】利用二次函数的性质和二次函数图象以及系数a、b、c的关系对题目进行判断即可得到答案,需要熟知增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC=
 ,反比例函数y=
,反比例函数y=  的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于 .
的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,等腰直角三角形OA1A2的直角边OA1在y轴的正半轴上,且OA1=A1A2=1,以OA2为直角边作第二个等腰直角三角形OA2A3 , 以OA3为直角边作第三个等腰直角三角形OA3A4 , …,依此规律,得到等腰直角三角形OA2017A2018 , 则点A2017的坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(﹣3,4),B(﹣5,2),C(﹣2,1).

(1)画出△ABC关于y轴对称图形△A1B1C1;
(2)画出将△ABC绕原点O逆时针方向旋转90°得到的△A2B2C2;
(3)求(2)中线段OA扫过的图形面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.

(1)求证:DE=DF,DE⊥DF;
(2)连接EF,若AC=10,求EF的长.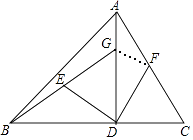
-
科目: 来源: 题型:
查看答案和解析>>【题目】为养成学生课外阅读的习惯,各学校普遍开展了“我的梦 中国梦”课外阅读活动,某校为了解七年级1200名学生课外日阅读所用时间情况,从中随机抽查了部分同学,进行了相关统计,整理并绘制出如下不完整的频数分布表和频数分布直方图,请根据图表信息解答下列问题:
组别
时间段(小时)
频数
频率
1
0≤x<0.5
10
0.05
2
0.5≤x<1.0
20
0.10
3
1.0≤x<1.5
80
b
4
1.5≤x<2.0
a
0.35
5
2.0≤x<2.5
12
0.06
6
2.5≤x<3.0
8
0.04

(1)表中a= , b=;
(2)请补全频数分布直方图中空缺的部分;
(3)样本中,学生日阅读所用时间的中位数落在第组;
(4)请估计该校七年级学生日阅读量不足1小时的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】“低碳环保,绿色出行”的理念得到广大群众的接受,越来越多的人再次选择自行车作为出行工具,小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图,请结合图象,解答下列问题:

(1)a= , b= , m= ;
(2)若小军的速度是120米/分,求小军在途中与爸爸第二次相遇时,距图书馆的距离;
(3)在(2)的条件下,爸爸自第二次出发至到达图书馆前,何时与小军相距100米?
(4)若小军的行驶速度是v米/分,且在途中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出v的取值范围.
相关试题

