Question

【题目】如图，菱形OABC的一边OA在x轴的负半轴上，O是坐标原点，tan∠AOC= ，反比例函数y= 的图象经过点C，与AB交于点D，若△COD的面积为20，则k的值等于 ．

Answer 1

【答案】﹣24
【解析】解：作DE∥AO，CF⊥AO，设CF=4x，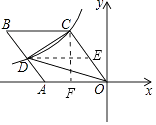
∵四边形OABC为菱形，
∴AB∥CO，AO∥BC，
∵DE∥AO，
∴S△ADO=S△DEO ，
同理S△BCD=S△CDE ，
∵S菱形ABCO=S△ADO+S△DEO+S△BCD+S△CDE ，
∴S菱形ABCO=2（S△DEO+S△CDE）=2S△CDO=40，
∵tan∠AOC= ，
∴OF=3x，
∴OC= =5x，
∴OA=OC=5x，
∵S菱形ABCO=AOCF=20x2 ， 解得：x= ，
∴OF= ，CF= ，
∴点C坐标为（﹣ ， ），
∵反比例函数y= 的图象经过点C，
∴代入点C得：k=﹣24，
所以答案是﹣24．
【考点精析】解答此题的关键在于理解比例系数k的几何意义的相关知识，掌握几何意义：表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积，以及对菱形的性质的理解，了解菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半．