【题目】如图,已知△ABC是等边三角形,D为边AC的中点,AE⊥EC,BD=EC.

(1)求证:△BDA≌△CEA;
(2)请判断△ADE是什么三角形,并说明理由.
参考答案:
【答案】(1)证明见解析;(2)△ADE是等边三角形,证明见解析.
【解析】
试题分析:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△BDA≌△CEA是解题的关键.(1)易证∠ACE=∠CBD,BC=AC,即可证明△BDA≌△CEA,即可解题;
(2)根据(1)中结论可得AE=CD,根据直角三角形中30°角所对直角边是斜边一半的性质可得DE=AD,即可解题.
试题解析:
(1)∵D是AC中点,
∴∠CBD=∠ABD=30°,∠BDA=90°,
∵∠ACB=60°,
∴∠ACE=30°,
在△BDA和△CEA中,
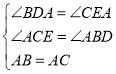 ,
,
∴△BDA≌△CEA(AAS);
(2)∵△BDA≌△CEA,
∴AE=CD,
∵RT△AEC中,∠ACE=30°,
∴DE=![]() AC=AD,
AC=AD,
∵AD=CD,
∴AD=DE=AE.
∴△ADE是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠MAN=120°,AC平分∠MAN.B、D分别在射线AN、AM上.
(1)在图1中,当∠ABC=∠ADC=90°时,求证:AD+AB=AC
(2)若把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°,其他条件不变,如图2所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.

(图1) (图2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,AB、AC是圆O的两条弦,AB=AC,过圆心O作OH⊥AC于点H.

(1)如图1,求证:∠B=∠C;
(2)如图2,当H、O、B三点在一条直线上时,求∠BAC的度数;
(3)如图3,在(2)的条件下,点E为劣弧BC上一点,CE=6,CH=7,连接BC、OE交于点D,求BE的长和
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商厦进货员预测一种应季衬衫能畅销市场,就用0.8万元购进这种衬衫,面市后果然供不应求.于是,商厦又用1.76万元购进了第二批这种衬衫,所购数量是第一批购进数量的2倍,但单价贵了4元,商厦销售这种衬衫时每件预定售价都是58元.
(1)求这种衬衫原进价为每件多少元?
(2)经过一段时间销售,根据市场饱和情况,商厦经理决定对剩余的100件衬衫进行打折销售,以提高回款速度,要使这两批衬衫的总利润不少于6300元,最多可以打几折?
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:2a2﹣8的结果为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,∠A=30°,CD为△ABC的中线,作CO⊥AB于O,点E在CO延长线上,DE=AD,连接BE、DE.

(1)求证:四边形BCDE为菱形;
(2)把△ABC分割成三个全等的三角形,需要两条分割线段,若AC=6,求两条分割线段长度的和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】a是不为1的有理数,我们把
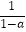 称为a的差倒数.如:2的差倒数是
称为a的差倒数.如:2的差倒数是 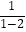 =﹣1,﹣1的差倒数是
=﹣1,﹣1的差倒数是 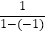 =
=  .已知a1=
.已知a1=  ,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推,则a2016= .
,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推,则a2016= .
相关试题

