搜索
【题目】
中，
，将线段AB绕点A按逆时针方向旋转
得到线段AD，其中
连结BD，CD，
．
若
，
，在图1中补全图形，并写出m值．
如图2，当
为钝角，
时，m值是否发生改变？证明你的猜想．
如图3，
，
，BD与AC相交于点O，求
与
的面积比．
参考答案：
【答案】（1）m=2（2）m值不发生改变（3）
【解析】
（1）如图1，根据旋转的性质得AB=AD，则AB=AD=AC，于是可判断点B、D、C在以点A为圆心、AB为半径的圆上，则根据圆周角定理可得∠DAC=2∠DBC，即有m=2；
（2）与（1）一样可判断点B、D、C在以点A为圆心、AB为半径的圆上，则根据圆周角定理可得∠DAC=2∠DBC，所以有m=2；
（3）作DH⊥AC于H，如图3，设AB=AC=AD=x，根据等腰直角三角形的性质得∠ABC=45°，利用（2）中的结论和∠DBC+∠DAC=45°可计算出∠DBC=15°，∠CAD=30°，则∠ABD=30°，在△ABO中，根据含30度的直角三角形三边的关系得OB=
，，所以OC=AC-A0=
，，在Rt△ADH中可计算出DH=
，，接着利用三角形面积公式可分别计算出S△OCD＝
，S△AOB=
，然后计算它们的比值．
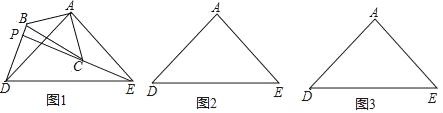
解：
如图，
线段AB绕点A按逆时针方向旋转
得到线段AD，
，
而
，
，
点B、D、C在以点A为圆心、AB为半径的圆上，
，
即
；
值不发生改变
理由与一样；
作
于H，如图3，
设
，
，，
，
，
而
，
，解得
，
，
，
在
中，
，
，
，
在
中，
，
，
，
，
：
：
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABF中，以AB为直径的圆分别交边AF、BF于C、E两点，CD⊥AF．AC是∠DAB的平分线，
（1）求证：直线CD是⊙O的切线．
（2）求证：△FEC是等腰三角形． -
科目： 来源： 题型：
查看答案和解析>>【题目】阅读资料：我们把顶点在圆上，并且一边和圆相交、另一边和圆相切的角叫做弦切角，如图1∠ABC所示．同学们研究发现：P为圆上任意一点，当弦AC经过圆心O时，且AB切⊙O于点A，此时弦切角∠CAB=∠P（图2）
证明：∵AB切⊙O于点A，∴∠CAB=90°，又∵AC是直径，∴∠P=90°∴∠CAB=∠P
问题拓展：若AC不经过圆心O（如图3），该结论：弦切角∠CAB=∠P还成立吗？请说明理由．
知识运用：如图4，AD是△ABC中∠BAC的平分线，经过点A的⊙O与BC切于点D，与AB、AC分别相交于E、F．求证：EF∥BC． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，反比例函数y=
（x＞0）的图象经过点A（2 
，1），射线AB与反比例函数图象交与另一点B（1，a），射线AC与y轴交于点C，∠BAC=75°，AD⊥y轴，垂足为D．
（1）求k和a的值；
（2）直线AC的解析式；
（3）如图3，M是线段AC上方反比例函数图象上一动点，过M作直线l⊥x轴，与AC相交于N，连接CM，求△CMN面积的最大值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，△ABC和△ADE是有公共顶点的等腰直角三角形，∠BAC=∠DAE=90°，EC的延长线交BD于点P．
（1）把△ABC绕点A旋转到图1，BD，CE的关系是 （选填“相等”或“不相等”）；简要说明理由；
（2）若AB=3，AD=5，把△ABC绕点A旋转，当∠EAC=90°时，在图2中作出旋转后的图形，PD= ，简要说明计算过程；
（3）在（2）的条件下写出旋转过程中线段PD的最小值为 ，最大值为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系
O
中，正方形A1B1C1O、A2B2C2B1、A3B3C3B2，…， 按图所示的方式放置．点A1、A2、A3，…和点B1、B2、B3，…分别在直线
和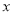
轴上．已知C1（1，-1），C2（
， 
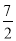），则点A3的坐标是________________________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】关于概率，下列说法正确的是（ ）
A.莒县“明天降雨的概率是75%”表明明天莒县会有75%的时间会下雨
B.随机抛掷一枚质地均匀的硬币，落地后一定反面向上
C.在一次抽奖活动中，中奖的概率是1%，则抽奖100次就一定会中奖
D.同时抛掷两枚质地均匀硬币，“一枚硬币正面向上，一枚硬币反面向上”的概率是
相关试题
