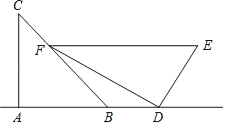
【题目】小敏是一位善于思考的学生,在一次数学活动课上,她将一副三角板按如图位置摆放,A、B、D在同一直线上,EF∥AD,∠BAC=∠EDF=90°,∠C=45°,∠E=60°,测得DE=8,则BD的长是( )
A. 10+4![]() B. 10﹣4
B. 10﹣4![]() C. 12﹣4
C. 12﹣4![]() D. 12+4
D. 12+4![]()
参考答案:
【答案】C
【解析】过E作EG⊥l于G,过F作FH⊥l于H,如图所示:
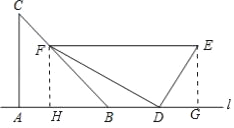
∵∠EFD=30°,∠EDF=90°,
∴∠FED=60°,
∴∠GED=30°,
∴GE=![]() DE=4
DE=4![]() cm,
cm,
∵EF∥AD,FH∥EG,
∴四边形EFHG是平行四边形,
∴FH=EG=4![]() .
.
∵∠C=45°,
∴BH=FH=4![]() ,
,
∵∠FDH=∠EFD=30°,
∴DH=![]() FH=12,
FH=12,
∴BD=(12﹣4![]() )cm.
)cm.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,BO、CO是角平分线.
(1)∠ABC=50°,∠ACB=60°,求∠BOC的度数,并说明理由.
(2)题(1)中,如将“∠ABC=50°,∠ACB=60°”改为“∠A=70°”,求∠BOC的度数.
(3)若∠A=n°,求∠BOC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=BC,∠ABC=120°,AC=2
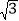 ,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )
,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )
A. y=
 x+4 B. y=
x+4 B. y=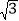 x+4 C. y=
x+4 C. y=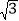 x2+4 D. y=
x2+4 D. y= x2+4
x2+4 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划组织师生共300人参加一次大型公益活动,如果租用6辆大客车和5辆小客车,恰好全部坐满,已知每辆大客车的乘客座位数比小客车多17个.
(1)求每辆大客车和每辆小客车的乘客座位数;
(2)由于最后参加活动的人数增加了30人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,且所有参加活动的师生都有座位,求租用小客车数量的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】7张如图1的长为
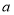 ,宽为b
,宽为b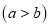 的小长方形纸片,按如图2、3的方式不重叠地放在 矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.
的小长方形纸片,按如图2、3的方式不重叠地放在 矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.
(1)如图2,点E、Q、P在同一直线上,点F、Q、G在同一直线上,右下角与左上角的阴影部分的面积的差为____________(用含
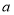 、
、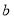 的代数式表示),矩形ABCD的面积为____________(用含
的代数式表示),矩形ABCD的面积为____________(用含 、
、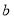 的代数式表示);
的代数式表示);(2)如图3,点F、H、Q、G在同一直线上,设右下角与左上角的阴影部分的面积的差为S,
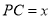 .
.①用
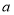 、
、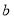 、
、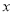 的代数式表示AE;
的代数式表示AE;②当BC的长度变化时,按照同样的放置方式,S始终保持不变,那么
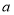 、
、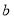 必须满足什么条件?
必须满足什么条件? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠B<90,BC>AB.作AE⊥BC于点E,AF⊥CD于点F,记∠EAF的度数为α,AE=a,AF=b.则以下选项错误的是( )

A. ∠D的度数为α
B. a∶b=CD∶BC
C. 若α=60,则平行四边形ABCD的周长为

D. 若α=60,则四边形AECF的面积为平行四边形ABCD面积的一半
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
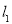 的解析式为
的解析式为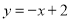 ,
,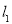 与
与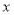 轴交于点
轴交于点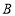 ,直线
,直线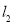 经过点
经过点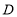 (0,5),与直线
(0,5),与直线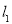 交于点
交于点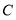 (﹣1,
(﹣1, ),且与
),且与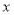 轴交于点
轴交于点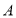 .
. (1)求点
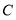 的坐标及直线
的坐标及直线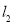 的解析式;
的解析式;(2)求△
 的面积.
的面积.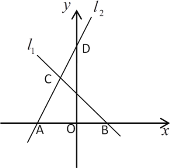
相关试题

