【题目】如图所示,在△ABC中,BO、CO是角平分线.
(1)∠ABC=50°,∠ACB=60°,求∠BOC的度数,并说明理由.
(2)题(1)中,如将“∠ABC=50°,∠ACB=60°”改为“∠A=70°”,求∠BOC的度数.
(3)若∠A=n°,求∠BOC的度数.

参考答案:
【答案】(1)125°;(2)125°;(3)∠BOC=90°+![]() n°.
n°.
【解析】
如图,由BO、CO是角平分线得∠ABC=2∠1,∠ACB=2∠2,再利用三角形内角和得到∠ABC+∠ACB+∠A=180°,则2∠1+2∠2+∠A=180°,接着再根据三角形内角和得到∠1+∠2+∠BOC=180°,利用等式的性质进行变换可得∠BOC=90°+![]() ∠A,然后根据此结论分别解决(1)、(2)、(3).
∠A,然后根据此结论分别解决(1)、(2)、(3).
如图,
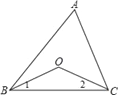
∵BO、CO是角平分线,
∴∠ABC=2∠1,∠ACB=2∠2,
∵∠ABC+∠ACB+∠A=180°,
∴2∠1+2∠2+∠A=180°,
∵∠1+∠2+∠BOC=180°,
∴2∠1+2∠2+2∠BOC=360°,
∴2∠BOC﹣∠A=180°,
∴∠BOC=90°+![]() ∠A,
∠A,
(1)∵∠ABC=50°,∠ACB=60°,
∴∠A=180°﹣50°﹣60°=70°,
∴∠BOC=90°+![]() ×70°=125°;
×70°=125°;
(2)∠BOC=90°+![]() ∠A=125°;
∠A=125°;
(3)∠BOC=90°+![]() n°.
n°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知图甲是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.
(1)你认为图乙中阴影部分的正方形的边长等于多少? .
(2)请用两种不同的方法求图乙中阴影部分的面积.
方法一: ;方法二: .
(3)观察图乙,你能写出下列三个代数式之间的等量关系吗?
(m+n)2;(m﹣n)2; mm
(4)根据(3)题中的等量关系,解决如下问题:若a+b=8,ab=5,求(a﹣b)2的值.

-
科目: 来源: 题型:
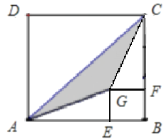
查看答案和解析>>【题目】如图,正方形ABCD与正方形BFGE中,点E在边AB上,若AE=a,BE=b,(其中a>2b).
(1)请用含有a,b的代数式表示图中阴影部分的面积;
(2)当a=5cm,b=3cm时,求阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,平面直角坐标系中,抛物线y=ax2+bx+3与x轴的两个交点分别为A(﹣3,0),B(1,0),与y轴的交点为D,对称轴与抛物线交于点C,与x轴负半轴交于点H.
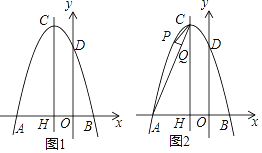
(1)求抛物线的表达式;
(2)点E,F分别是抛物线对称轴CH上的两个动点(点E在点F上方),且EF=1,求使四边形BDEF的周长最小时的点E,F坐标及最小值;
(3)如图2,点P为对称轴左侧,x轴上方的抛物线上的点,PQ⊥AC于点Q,是否存在这样的点P使△PCQ与△ACH相似?若存在请求出点P的坐标,若不存在请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=BC,∠ABC=120°,AC=2
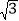 ,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )
,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )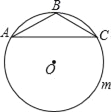
A. y=
 x+4 B. y=
x+4 B. y=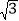 x+4 C. y=
x+4 C. y=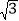 x2+4 D. y=
x2+4 D. y= x2+4
x2+4 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划组织师生共300人参加一次大型公益活动,如果租用6辆大客车和5辆小客车,恰好全部坐满,已知每辆大客车的乘客座位数比小客车多17个.
(1)求每辆大客车和每辆小客车的乘客座位数;
(2)由于最后参加活动的人数增加了30人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,且所有参加活动的师生都有座位,求租用小客车数量的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小敏是一位善于思考的学生,在一次数学活动课上,她将一副三角板按如图位置摆放,A、B、D在同一直线上,EF∥AD,∠BAC=∠EDF=90°,∠C=45°,∠E=60°,测得DE=8,则BD的长是( )
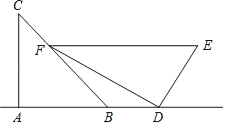
A. 10+4
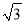 B. 10﹣4
B. 10﹣4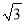 C. 12﹣4
C. 12﹣4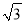 D. 12+4
D. 12+4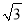
相关试题

