搜索
【题目】在ABCD中，∠ACB=25°，现将ABCD沿EF折叠，使点C与点A重合，点D落在G处，则∠GFE的度数（ ）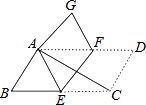 
A.135°
B.120°
C.115°
D.100°
参考答案：
【答案】C
【解析】解：由折叠可得：∠EAC=∠ECA=25°，∠FEC=∠AEF，∠DFE=∠GFE， ∵∠EAC+∠ECA+∠AEC=180°，
∴∠AEC=130°，
∴∠FEC=65°，
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠DFE+∠FEC=180°，
∴∠DFE=115°，
∴∠GFE=115°，
故选：C．
首先根据折叠找到对应相等的角∠EAC=∠ECA=25°，∠FEC=∠AEF，∠DFE=∠GFE，然后根据三角形内角和可算出∠AEC，进而可得∠FEC的度数，再根据平行四边形的性质可得∠DFE=115°，进而可得答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了了解一路段车辆行驶速度的情况，交警统计了该路段上午7：：0至9：00来往车辆的车速（单位：千米/时），并绘制成如图所示的条形统计图．这些车速的众数、中位数分别是（ ）
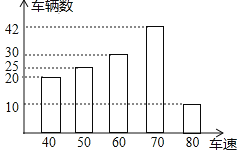
A. 众数是80千米
时，中位数是60千米时B. 众数是70千米
时，中位数是70千米时C. 众数是60千米
时，中位数是60千米时D. 众数是70千米
时，中位数是60千米时 -
科目： 来源： 题型：
查看答案和解析>>【题目】希望中学开展以“我最喜欢的职业”为主题的调查活动，通过对学生的随机抽样调查得到一组数据，如图是根据这组数据绘制的不完整的统计图，则下列说法中，不正确的是（ ）
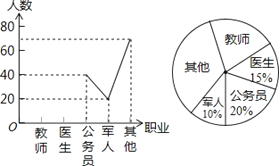
A. 被调查的学生有200人
B. 被调查的学生中喜欢教师职业的有40人
C. 被调查的学生中喜欢其他职业的占40%
D. 扇形图中，公务员部分所对应的圆心角为72°
-
科目： 来源： 题型：
查看答案和解析>>【题目】某电子元件厂准备生产4600个电子元件，甲车间独立生产一半后，由于要尽快投入市场，乙车间也加入了该电子元件的生产．若乙车间每天生产的电子元件的个数是甲车间每天生产的电子元件的个数的1.3倍，结果共用33天完成了任务．问：甲车间每天生产电子元件多少个？在这个问题中设甲车间每天生产电子元件x个，根据题意可列方程为______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】小明随机调查了若干市民租用公共自行车的骑车时间t（单位：分），将获得的数据分成四组，绘制了如下统计图。请根据图中信息，解答下列问题：
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/12/1922393511583744/1923977001213952/STEM/d5900c7cb9b84a9a89aefef7d82bcf93.png]
（1）这次被调查的总人数是多少？
（2）试求表示A组的扇形圆心角的度数，并补全条形统计图；
（3）如果骑自行车的平均速度为12km/h，请估算，在租用公共自行车的市民中，骑车路程不超过6km的人数所占的百分比。
-
科目： 来源： 题型：
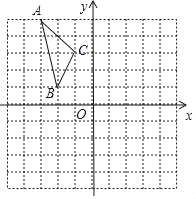
查看答案和解析>>【题目】如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣3，5），B（﹣2，1），C（﹣1，3）．
（1）画出△ABC和△A1B1C1关于原点O对称，画出△A1B1C1，并写出△A1B1C1的各顶点的坐标；
（2）将△ABC绕着点O按顺时针方向旋转90°得到的△A2B2C2，画出△A2B2C2，并写出△A2B2C2的各顶点的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知矩形ABCD，AD=9，AB=6，若点G、H、M、N分别在AB、CD、AD、BC上，线段MN与GH交于点K．若∠GKM=45°，NM=3
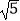，则GH= ．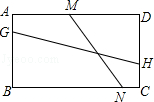 
相关试题
