【题目】如图,已知矩形ABCD,AD=9,AB=6,若点G、H、M、N分别在AB、CD、AD、BC上,线段MN与GH交于点K.若∠GKM=45°,NM=3 ![]() ,则GH= .
,则GH= . 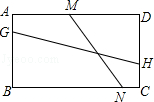
参考答案:
【答案】3 ![]()
【解析】解:如图,过点A作AE∥GH交CD于E,作AF∥MN交BC于F, 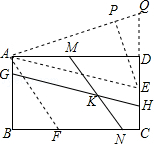
则AF=MN=3 ![]() ,AE=GH,
,AE=GH,
∵∠GKM=45°,
∴∠BAF+∠DAE=90°﹣45°=45°,
作∠QAE=45°交CD的延长线于Q,
则∠QAD+∠DAE=45°,
∴∠QAD=∠FAB,
∵∠B=∠ADQ=90°,
∴△ABF∽△AQD,
∴ ![]() ,
,
∴ ![]() ,
,
∴AQ= ![]() ,
,
在Rt△ADQ中,DQ= ![]() =
= ![]() ,
,
过点E作EP⊥AQ于P,
∵∠QAE=45°,
∴△AEP是等腰直角三角形,
设GH=AE=x,则AP=EP= ![]() AE=
AE= ![]() x,
x,
∵tan∠Q= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得x=3 ![]() ,
,
所以GH=3 ![]() .
.
故答案为:3 ![]() .
.
过点A作AE∥GH交CD于E,作AF∥MN交BC于F,于是得到AF=MN=3 ![]() ,AE=GH,由于∠GKM=45°,得到∠BAF+∠DAE=90°﹣45°=45°,作∠QAE=45°交CD的延长线于Q,推出∠QAD+∠DAE=45°,通过△ABF≌△AQD,根据相似三角形的性质得到
,AE=GH,由于∠GKM=45°,得到∠BAF+∠DAE=90°﹣45°=45°,作∠QAE=45°交CD的延长线于Q,推出∠QAD+∠DAE=45°,通过△ABF≌△AQD,根据相似三角形的性质得到 ![]() ,求得AQ=
,求得AQ= ![]() ,在Rt△ADQ中,由勾股定理得到DQ=
,在Rt△ADQ中,由勾股定理得到DQ= ![]() =
= ![]() ,过点E作EP⊥AQ于P,得到△AEP是等腰直角三角形,设GH=AE=x,则AP=EP=
,过点E作EP⊥AQ于P,得到△AEP是等腰直角三角形,设GH=AE=x,则AP=EP= ![]() AE=
AE= ![]() ,然后利用∠Q的正切值列出方程求解即可.
,然后利用∠Q的正切值列出方程求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,∠ACB=25°,现将ABCD沿EF折叠,使点C与点A重合,点D落在G处,则∠GFE的度数( )
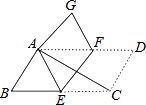
A.135°
B.120°
C.115°
D.100° -
科目: 来源: 题型:
查看答案和解析>>【题目】小明随机调查了若干市民租用公共自行车的骑车时间t(单位:分),将获得的数据分成四组,绘制了如下统计图。请根据图中信息,解答下列问题:
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/12/1922393511583744/1923977001213952/STEM/d5900c7cb9b84a9a89aefef7d82bcf93.png]
(1)这次被调查的总人数是多少?
(2)试求表示A组的扇形圆心角的度数,并补全条形统计图;
(3)如果骑自行车的平均速度为12km/h,请估算,在租用公共自行车的市民中,骑车路程不超过6km的人数所占的百分比。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)画出△ABC和△A1B1C1关于原点O对称,画出△A1B1C1,并写出△A1B1C1的各顶点的坐标;
(2)将△ABC绕着点O按顺时针方向旋转90°得到的△A2B2C2,画出△A2B2C2,并写出△A2B2C2的各顶点的坐标.
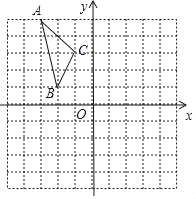
-
科目: 来源: 题型:
查看答案和解析>>【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
月均用水量/t
频数
百分比
2≤x<3
2
4%
3≤x<4
12
24%
4≤x<5
5≤x<6
10
20%
6≤x<7
12%
7≤x<8
3
6%
8≤x<9
2
4%

(2)如果家庭月均用水量“大于或等于4 t且小于7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知点A、B是反比例函数y=﹣
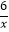 上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为 .
上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为 . 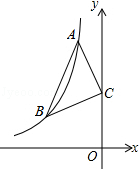
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为4的菱形ABCD中,∠A=60°,M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,则线段A′C长度的最小值是 .

相关试题

