【题目】实验探究:
(1)如图1,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开;再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN,MN.请你观察图1,猜想∠MBN的度数是多少,并证明你的结论. 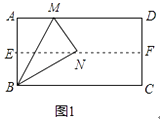
(2)将图1中的三角形纸片BMN剪下,如图2,折叠该纸片,探究MN与BM的数量关系,写出折叠方案,并结合方案证明你的结论. 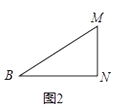
参考答案:
【答案】
(1)解:猜想:∠MBN=30°.
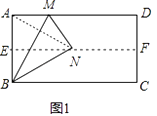
理由:如图1中,连接AN,∵直线EF是AB的垂直平分线,
∴NA=NB,
由折叠可知,BN=AB,
∴AB=BN=AN,
∴△ABN是等边三角形,
∴∠ABN=60°,
∴NBM=∠ABM= ![]() ∠ABN=30°.
∠ABN=30°.
(2)解:结论:MN= ![]() BM.
BM.
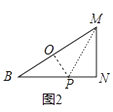
折纸方案:如图2中,折叠△BMN,使得点N落在BM上O处,折痕为MP,连接OP.
理由:由折叠可知△MOP≌△MNP,
∴MN=OM,∠OMP=∠NMP= ![]() ∠OMN=30°=∠B,
∠OMN=30°=∠B,
∠MOP=∠MNP=90°,
∴∠BOP=∠MOP=90°,
∵OP=OP,
∴△MOP≌△BOP,
∴MO=BO= ![]() BM,
BM,
∴MN= ![]() BM.
BM.
【解析】(1)猜想:∠MBN=30°.只要证明△ABN是等边三角形即可;(2)结论:MN= ![]() BM.折纸方案:如图,折叠△BMN,使得点N落在BM上O处,折痕为MP,连接OP.由折叠可知△MOP≌△MNP,只要证明△MOP≌△BOP,即可推出MO=BO=
BM.折纸方案:如图,折叠△BMN,使得点N落在BM上O处,折痕为MP,连接OP.由折叠可知△MOP≌△MNP,只要证明△MOP≌△BOP,即可推出MO=BO= ![]() BM;
BM;
-
科目: 来源: 题型:
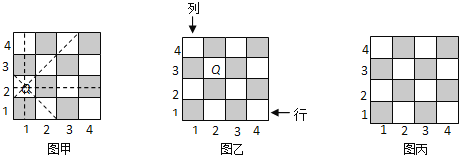
查看答案和解析>>【题目】国际象棋、中国象棋和围棋号称世界三大棋种. 国际象棋中的“皇后”的威力可比中国象棋中的“车”大得多:“皇后”不仅能控制她所在的行与列中的每一个小方格,而且还能控制“斜”方向的两条直线上的每一个小方格.如图甲是一个4×4的小方格棋盘,图中的“皇后Q”能控制图中虚线所经过的每一个小方格.
(1)在如图乙的小方格棋盘中有一“皇后Q”,她所在的位置可用“(2,3)”来表示,请说明“皇后Q”所在的位置“(2,3)”的意义,并用这种表示法分别写出棋盘中不能被该“皇后Q”所控制的四个位置.
(2)如图丙也是一个4×4的小方格棋盘,请在这个棋盘中放入四个“皇后Q”,使这四个“皇后Q”之间互不受对方控制(在图丙中的某四个小方格中标出字母Q即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的直径AB=12,弦AC=10,D是
 的中点,过点D作DE⊥AC,交AC的延长线于点E.
的中点,过点D作DE⊥AC,交AC的延长线于点E. 
(1)求证:DE是⊙O的切线;
(2)求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在“母亲节”前期,某花店购进康乃馨和玫瑰两种鲜花,销售过程中发现康乃馨比玫瑰销售量大,店主决定将玫瑰每枝降价1元促销,降价后30元可购买玫瑰的数量是原来购买玫瑰数量的1.5倍,求降价后每枝玫瑰的售价是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=mx2﹣(2m﹣5)x+m﹣2的图象与x轴有两个公共点.
(1)求m的取值范围,并写出当m取范围内最大整数时函数的解析式;
(2)题(1)中求得的函数记为C1 ,
①当n≤x≤﹣1时,y的取值范围是1≤y≤﹣3n,求n的值;
②函数C2:y=m(x﹣h)2+k的图象由函数C1的图象平移得到,其顶点P落在以原点为圆心,半径为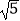 的圆内或圆上,设函数C1的图象顶点为M,求点P与点M距离最大时函数C2的解析式.
的圆内或圆上,设函数C1的图象顶点为M,求点P与点M距离最大时函数C2的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:点P是△ABC内部或边上的点(顶点除外),在△PAB,△PBC,△PCA中,若至少有一个三角形与△ABC相似,则称点P是△ABC的自相似点.
例如:如图1,点P在△ABC的内部,∠PBC=∠A,∠PCB=∠ABC,则△BCP∽△ABC,故点P是△ABC的自相似点.
请你运用所学知识,结合上述材料,解决下列问题:
在平面直角坐标系中,点M是曲线y=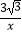 (x>0)上的任意一点,点N是x轴正半轴上的任意一点.
(x>0)上的任意一点,点N是x轴正半轴上的任意一点.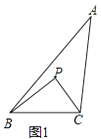
(1)如图2,点P是OM上一点,∠ONP=∠M,试说明点P是△MON的自相似点;当点M的坐标是(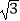 ,3),点N的坐标是(
,3),点N的坐标是( 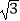 ,0)时,求点P的坐标;
,0)时,求点P的坐标;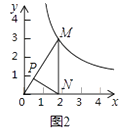
(2)如图3,当点M的坐标是(3,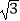 ),点N的坐标是(2,0)时,求△MON的自相似点的坐标;
),点N的坐标是(2,0)时,求△MON的自相似点的坐标;
(3)是否存在点M和点N,使△MON无自相似点?若存在,请直接写出这两点的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)通过计算下列各式的值探究问题:
①
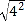 = ;
= ;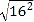 = ;
= ;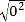 = ;
= ;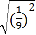 = .
= .探究:对于任意非负有理数a,
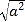 = .
= .②
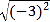 = ;
= ;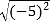 = ;
= ;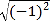 = ;
= ;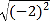 = .
= .探究:对于任意负有理数a,
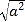 = .
= .综上,对于任意有理数a,
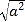 = .
= .(2)应用(1)所得的结论解决问题:有理数a,b在数轴上对应的点的位置如图所示,化简:
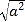 -
-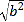 -
-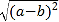 +|a+b|.
+|a+b|.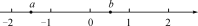
相关试题

