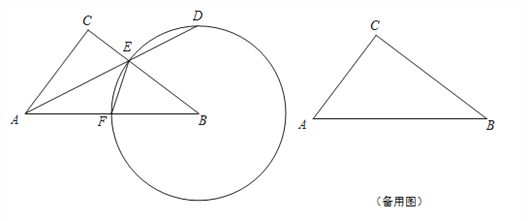
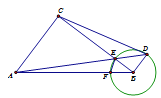
【题目】如图,已知在Rt△ABC中,∠ACB = 90o,AC =6,BC = 8,点F在线段AB上,以点B为圆心,BF为半径的圆交BC于点E,射线AE交圆B于点D(点D、E不重合).
(1)如果设BF = x,EF = y,求y与x之间的函数关系式,并写出它的定义域;
(2)如果![]() ,求ED的长;
,求ED的长;
(3)联结CD、BD,请判断四边形ABDC是否为直角梯形?说明理由.
参考答案:
【答案】(1)![]() (0<x<8);(2)ED=
(0<x<8);(2)ED=![]() ;(3)四边形ABDC不可能为直角梯形.
;(3)四边形ABDC不可能为直角梯形.
【解析】试题分析:(1)在Rt△ABC中由勾股定理得到AB=10.过E作EH⊥AB,垂足是H,易得:EH= ![]() ,BH=
,BH= ![]() ,FH=
,FH= ![]() .在Rt△EHF中,由勾股定理即可得到结论;
.在Rt△EHF中,由勾股定理即可得到结论;
(2)取弧ED的中点P,联结BP交ED于点G.由![]() ,P是弧ED的中点,得到弧EP=弧EF=弧PD,进而得到∠FBE =∠EBP =∠PBD.由垂径定理得BG⊥ED,ED =2EG =2DG.易证△BEH≌△BEG,得到EH=EG=GD=
,P是弧ED的中点,得到弧EP=弧EF=弧PD,进而得到∠FBE =∠EBP =∠PBD.由垂径定理得BG⊥ED,ED =2EG =2DG.易证△BEH≌△BEG,得到EH=EG=GD= ![]() .解Rt△CEA得到CE,BE的长,从而得到结论.
.解Rt△CEA得到CE,BE的长,从而得到结论.
(3)四边形ABDC不可能为直角梯形.分两种情况讨论:①当CD∥AB时,如果四边形ABDC是直角梯形,只可能∠ABD =∠CDB = 90o.由![]() ,即可得到结论.
,即可得到结论.
②当AC∥BD时,如果四边形ABDC是直角梯形,只可能∠ACD =∠CDB = 90o.由∠ABD> 90o.即可得到结论.
试题解析:解:(1)在Rt△ABC中,AC=6,BC=8,∠ACB=90°,∴AB=10.
过E作EH⊥AB,垂足是H,易得:EH= ![]() ,BH=
,BH= ![]() ,FH=
,FH= ![]() .
.
在Rt△EHF中, ![]() ,∴
,∴![]() (0<x<8).
(0<x<8).
(2)取弧ED的中点P,联结BP交ED于点G.
∵![]() ,P是弧ED的中点,∴弧EP=弧EF=弧PD,∴∠FBE =∠EBP =∠PBD.
,P是弧ED的中点,∴弧EP=弧EF=弧PD,∴∠FBE =∠EBP =∠PBD.
∵弧EP=弧EF ,BP过圆心,∴BG⊥ED,ED =2EG =2DG.
又∵∠CEA =∠DEB,∴∠CAE=∠EBP=∠ABC.
又∵BE是公共边,∴△BEH≌△BEG,∴EH=EG=GD= ![]() .
.
在Rt△CEA中,∵AC = 6,BC=8,tan∠CAE=tan∠ABC=![]() ,∴CE=ACtan∠CAE=
,∴CE=ACtan∠CAE=![]() =
=![]() ,∴BE=
,∴BE=![]() =
=![]() ,∴ED=2EG=
,∴ED=2EG= ![]() =
=![]() =
=![]() .
.
(3)四边形ABDC不可能为直角梯形.
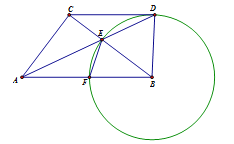
①当CD∥AB时,如果四边形ABDC是直角梯形,只可能∠ABD =∠CDB = 90o.
在Rt△CBD中,∵BC=8,∴CDcos∠BCD=![]() ,BD=BCsin∠BCD=
,BD=BCsin∠BCD=![]() =BE,∴
=BE,∴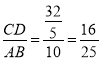 ,
, 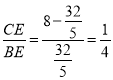 ,∴
,∴![]() ,∴CD不平行于AB,与CD∥AB矛盾,∴四边形ABDC不可能为直角梯形.
,∴CD不平行于AB,与CD∥AB矛盾,∴四边形ABDC不可能为直角梯形.
②当AC∥BD时,如果四边形ABDC是直角梯形,只可能∠ACD =∠CDB = 90o.
∵AC∥BD,∠ACB = 90o,∴∠ACB =∠CBD = 90o,∴∠ABD =∠ACB +∠BCD > 90o.
与∠ACD =∠CDB = 90o矛盾.
∴四边形ABDC不可能为直角梯形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
 x2﹣x+4与x轴交于A,B两点(A在B的左侧),与y轴交于点C.
x2﹣x+4与x轴交于A,B两点(A在B的左侧),与y轴交于点C.(1)求点A,点B的坐标;
(2)求△ABC的面积;
(3)P为第二象限抛物线上的一个动点,求△ACP面积的最大值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在平面直角坐标系xOy中,抛物线y=ax2﹣2x+c与x轴交于点A和点B(1,0),与y轴相交于点C(0,3).
(1)求抛物线的解析式和顶点D的坐标;
(2)求证:∠DAB=∠ACB;
(3)点Q在抛物线上,且△ADQ是以AD为底的等腰三角形,求Q点的坐标.

-
科目: 来源: 题型:
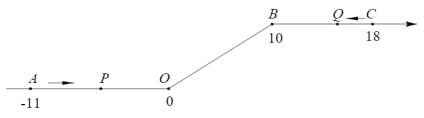
查看答案和解析>>【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条 “折线数轴” .图中点A表示-11,点B表示10,点C表示18,我们称点A和点C在数轴上相距29个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.
问:(1)动点P从点A运动至C点需要多少时间?
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少;
(3)求当t为何值时,P、B两点在数轴上相距的长度与Q、O两点在数轴上相距的长度相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】年是我市“创建国家卫生城市”第一年,为了了解本班
 名学生对“创卫”的知晓率,某同学采取随机抽样的方法进行问卷调查,调查分为四个选项:
名学生对“创卫”的知晓率,某同学采取随机抽样的方法进行问卷调查,调查分为四个选项: 非常了解,
非常了解, 比较了解,
比较了解, 基本了解,
基本了解, 不甚了解.数据整理如下:
不甚了解.数据整理如下:







请画出条形图和扇形图来描述以上统计数据.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(-1,0);⑤当1<x<4时,有y2<y1,
其中正确的是( )

A. ①②③ B. ①③④ C. ①③⑤ D. ②④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校计划组织全校1441名师生到相关部门规划的林区植树,经过研究,决定租用当地租车公司一共62辆
 两种型号客车作为交通工具.
两种型号客车作为交通工具.下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
型号
载客量
租金单价

30人/辆
380元/辆

20人/辆
280元/辆
注:载客量指的是每辆客车最多可载该校师生的人数.设学校租用
 型号客车
型号客车 辆,租车总费用为
辆,租车总费用为 元.
元.(1)求
 与
与 的函数解析式,请直接写出
的函数解析式,请直接写出 的取值范围;
的取值范围;(2)若要使租车总费用不超过21940元,一共有几种租车方案?哪种租车方案总费用最省?最省的总费用是多少?
相关试题

