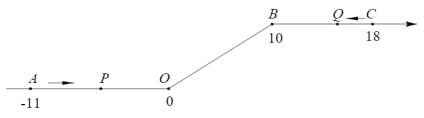
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条 “折线数轴” .图中点A表示-11,点B表示10,点C表示18,我们称点A和点C在数轴上相距29个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.
问:(1)动点P从点A运动至C点需要多少时间?
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少;
(3)求当t为何值时,P、B两点在数轴上相距的长度与Q、O两点在数轴上相距的长度相等.
参考答案:
【答案】(1)19.5;(2)5;(3)t的值为:3或6.75或10.5或18.
【解析】
(1)根据路程除以速度等于时间,可得答案;
(2)根据相遇时P,Q的时间相等,可得方程,根据解方程,可得答案;
(3)根据PO与BQ的时间相等,可分为四种情况进行分析,分别列出方程,根据解方程,即可得到答案.
解:(1)点P运动至点C时,所需时间:t=11÷2+10÷1+8÷2=19.5(秒),
∴动点P从点A运动至C点需要19.5秒;
(2)由题可知,P、Q两点相遇在线段OB上于M处,设OM=x.
则11÷2+x÷1=8÷1+(10-x)÷2,
解得:x=5,
∴M所对应的数为5;
(3)P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等有4种可能:
①动点Q在CB上,动点P在AO上,
则:8-t=11-2t,
解得:t=3.
②动点Q在CB上,动点P在OB上,
则:8-t=(t-5.5)×1,
解得:t=6.75.
③动点Q在BO上,动点P在OB上,
则:2(t-8)=(t-5.5)×1,
解得:t=10.5.
④动点Q在OA上,动点P在BC上,
则:10+2(t-15.5)=t-13+10,
解得:t=18,
综上所述,t的值为:3或6.75或10.5或18.
-
科目: 来源: 题型:
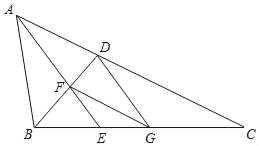
查看答案和解析>>【题目】如图,已知在△ABC中,∠BAC=2∠C,∠BAC的平分线AE与∠ABC的平分线BD相交于点F,FG∥AC,联结DG.
(1)求证:BFBC=ABBD;
(2)求证:四边形ADGF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
 x2﹣x+4与x轴交于A,B两点(A在B的左侧),与y轴交于点C.
x2﹣x+4与x轴交于A,B两点(A在B的左侧),与y轴交于点C.(1)求点A,点B的坐标;
(2)求△ABC的面积;
(3)P为第二象限抛物线上的一个动点,求△ACP面积的最大值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在平面直角坐标系xOy中,抛物线y=ax2﹣2x+c与x轴交于点A和点B(1,0),与y轴相交于点C(0,3).
(1)求抛物线的解析式和顶点D的坐标;
(2)求证:∠DAB=∠ACB;
(3)点Q在抛物线上,且△ADQ是以AD为底的等腰三角形,求Q点的坐标.

-
科目: 来源: 题型:
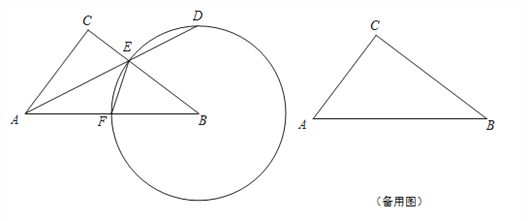
查看答案和解析>>【题目】如图,已知在Rt△ABC中,∠ACB = 90o,AC =6,BC = 8,点F在线段AB上,以点B为圆心,BF为半径的圆交BC于点E,射线AE交圆B于点D(点D、E不重合).
(1)如果设BF = x,EF = y,求y与x之间的函数关系式,并写出它的定义域;
(2)如果
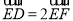 ,求ED的长;
,求ED的长;(3)联结CD、BD,请判断四边形ABDC是否为直角梯形?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】年是我市“创建国家卫生城市”第一年,为了了解本班
 名学生对“创卫”的知晓率,某同学采取随机抽样的方法进行问卷调查,调查分为四个选项:
名学生对“创卫”的知晓率,某同学采取随机抽样的方法进行问卷调查,调查分为四个选项: 非常了解,
非常了解, 比较了解,
比较了解, 基本了解,
基本了解, 不甚了解.数据整理如下:
不甚了解.数据整理如下:







请画出条形图和扇形图来描述以上统计数据.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(-1,0);⑤当1<x<4时,有y2<y1,
其中正确的是( )

A. ①②③ B. ①③④ C. ①③⑤ D. ②④⑤
相关试题

