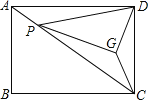
【题目】如图,在矩形ABCD中,AB=3,BC=4,P是对角线AC上的动点,连接DP,将直线DP绕点P顺时针旋转使∠DPG=∠DAC,且过D作DG⊥PG,连接CG,则CG最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】D
【解析】
如图,作DH⊥AC于H,连接HG延长HG交CD于F,作HE⊥CD于H.证明△ADP∽△DHG,推出∠DHG=∠DAP=定值,推出点G在射线HF上运动,推出当CG⊥HE时,CG的值最小,想办法求出CG即可.
如图,作DH⊥AC于H,连接HG延长HG交CD于F,作HE⊥CD于H.
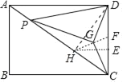
∵DG⊥PG,DH⊥AC,
∴∠DGP=∠DHA,
∵∠DPG=∠DAH,
∴△ADH∽△PDG,
∴![]() ,∠ADH=∠PDG,
,∠ADH=∠PDG,
∴∠ADP=∠HDG,
∴△ADP∽△DHG,
∴∠DHG=∠DAP=定值,
∴点G在射线HF上运动,
∴当CG⊥HE时,CG的值最小,
∵四边形ABCD是矩形,
∴∠ADC=90°,
∴∠ADH+∠HDF=90°,
∵∠DAH+∠ADH=90°,
∴∠HDF=∠DAH=∠DHF,
∴FD=FH,
∵∠FCH+∠CDH=90°,∠FHC+∠FHD=90°,
∴∠FHC=∠FCH,
∴FH=FC=DF=3,
在Rt△ADC中,∵∠ADC=90°,AD=4,CD=3,
∴AC=![]() =5,DH=
=5,DH=![]() ,
,
∴CH=![]() ,
,
∴EH=![]() ,
,
∵∠CFG=∠HFE,∠CGF=∠HEF=90°,CF=HF,
∴△CGF≌△HEF(AAS),
∴CG=HE=![]() ,
,
∴CG的最小值为![]() ,
,
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱.各种品牌的山地车相继投放市场.顺风车行经营的
 型车2018年6月份销售总额为
型车2018年6月份销售总额为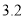 万元,今年经过改造升级后
万元,今年经过改造升级后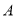 型车每辆销售价比去年增加
型车每辆销售价比去年增加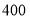 元,若今年6月份与去年6月份卖出的
元,若今年6月份与去年6月份卖出的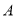 型车数量相同,则今年6月份
型车数量相同,则今年6月份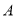 型车销售总额将比去年6月份销售总额增加
型车销售总额将比去年6月份销售总额增加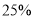 .
.(1)今年6月份
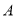 型车每辆售价多少元?(用列方程的方法解答)
型车每辆售价多少元?(用列方程的方法解答)(2)已知
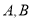 两种型号车今年的进货及销售价格如下表:
两种型号车今年的进货及销售价格如下表: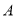 型车
型车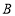 型车
型车进货价格(元/辆)
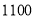
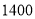
销售价格(元/辆)
今年的销售价格
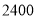
该车行计划7月份进这批
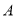 型车和
型车和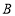 型车共
型车共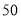 辆,且
辆,且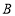 型车的进货数量不超过
型车的进货数量不超过 型车数量的两倍,应如何进货才能是这批车获利最多?
型车数量的两倍,应如何进货才能是这批车获利最多? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=﹣kx+k与反比例函数y=﹣
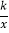 (k≠0)在同一坐标系中的图象可能是( )
(k≠0)在同一坐标系中的图象可能是( )A.
 B.
B. 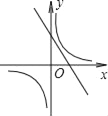 C.
C.  D.
D. 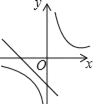
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A=a2-2ab+b2,B=a2+2ab+b2.
(1)求A+B;
(2)求
 (A+B);
(A+B);(3)如果2A-3B+C=0,那么C的表达式是什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论中一定成立的是( )
①OG=
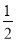 AB;②与△EGD全等的三角形共有5个;③S四边形ODGF>S△ABF;④由点A、B、D、E构成的四边形是菱形.
AB;②与△EGD全等的三角形共有5个;③S四边形ODGF>S△ABF;④由点A、B、D、E构成的四边形是菱形.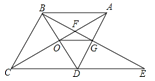
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
甲、乙两人同时从相距25千米的A地去B 地,甲骑车乙步行,甲的速度是乙的速度的3倍,甲到达B地停留40分钟,然后从B地返回A地,在途中遇见乙,这时距他们出发的时间恰好3小时,求两人的速度各是多少?
相关试题

