【题目】已知抛物线![]() 与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).
与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).
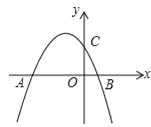
(1)求抛物线的解析式;
(2)已知点P在抛物线上,连接PC,PB,若△PBC是以BC为直角边的直角三角形,求点P的坐标;
(3)已知点E在x轴上,点F在抛物线上,是否存在以A,C,E,F为顶点的四边形是平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)满足条件的P点坐标为(﹣4,0),P2(﹣5,﹣3);
;(2)满足条件的P点坐标为(﹣4,0),P2(﹣5,﹣3);
(3)E为(﹣7,0)或(﹣1,0)或(![]() ,﹣2)或(
,﹣2)或(![]() ,﹣2).
,﹣2).
【解析】
试题分析:(1)因为抛物线经过点A(﹣4,0),B(1,0),所以可以设抛物线为y=﹣![]() (x+4)(x﹣1),展开即可解决问题.
(x+4)(x﹣1),展开即可解决问题.
(2)先证明∠ACB=90°,点A就是所求的点P,求出直线AC解析式,再求出过点B平行AC的直线的解析式,利用方程组即可解决问题.
(3)分AC为平行四边形的边,AC为平行四边形的对角线两种切线讨论即可解决问题.
试题解析:(1)抛物线的解析式为y=﹣![]() (x+4)(x﹣1),即
(x+4)(x﹣1),即![]() ;
;
(2)存在.
当x=0,y═![]() =2,则C(0,2),
=2,则C(0,2),
∴OC=2,
∵A(﹣4,0),B(1,0),
∴OA=4,OB=1,AB=5,
当∠PCB=90°时,
∵AC2=42+22=20,BC2=22+12=5,AB2=52=25
∴AC2+BC2=AB2
∴△ACB是直角三角形,∠ACB=90°,
∴当点P与点A重合时,△PBC是以BC为直角边的直角三角形,此时P点坐标为(﹣4,0);
当∠PBC=90°时,PB∥AC,如图1,
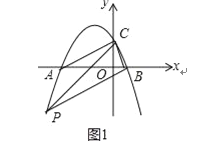
设直线AC的解析式为y=mx+n,
把A(﹣4,0),C(0,2)代入得![]() ,解得
,解得 ,
,
∴直线AC的解析式为y=![]() x+2,
x+2,
∵BP∥AC,
∴直线BP的解析式为y=![]() x+p,
x+p,
把B(1,0)代入得![]() +p=0,解得p=﹣
+p=0,解得p=﹣![]() ,
,
∴直线BP的解析式为y=![]() x﹣
x﹣![]() ,
,
解方程组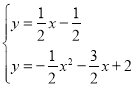 得
得![]() 或
或![]() ,此时P点坐标为(﹣5,﹣3);
,此时P点坐标为(﹣5,﹣3);
综上所述,满足条件的P点坐标为(﹣4,0),P2(﹣5,﹣3);
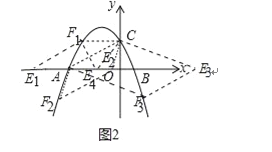
(3)存在点E,设点E坐标为(m,0),F(n,![]() )
)
①当AC为边,CF1∥AE1,易知CF1=3,此时E1坐标(﹣7,0),
②当AC为边时,AC∥EF,易知点F纵坐标为﹣2,
∴![]() =﹣2,解得n=
=﹣2,解得n=![]() ,得到F2(
,得到F2(![]() ,﹣2),F3(
,﹣2),F3(![]() ,﹣2),
,﹣2),
因此m=![]() 或
或![]() ,
,
此时E2(![]() ,0),E3(
,0),E3(![]() ,0),
,0),
③当AC为对角线时,AE4=CF1=3,此时E4(﹣1,0),
综上所述满足条件的点E为(﹣7,0)或(﹣1,0)或(![]() ,﹣2)或(
,﹣2)或(![]() ,﹣2).
,﹣2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】若﹣|a|=﹣3.2,则a是( )
A. 3.2 B. ﹣3.2 C. ±3.2 D. 以上都不对
-
科目: 来源: 题型:
查看答案和解析>>【题目】教练组对运动员正式比赛前的5次训练成绩进行分析,判断谁的成绩更加稳定,一般需要考察这5次成绩的 ( )
A. 平均数或中位数 B. 众数或频率 C. 方差或极差 D. 频数或众数
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程(k﹣1)(k﹣2)x2+(k﹣1)x+5=0.
求:(1)当k为何值时,原方程是一元二次方程;
(2)当k为何值时,原方程是一元一次方程,并求出此时方程的解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,正确的是( )
A. a6÷a3=a2 B. a3a2=a5 C. (a+b)2=a2+b2 D. 2a+3b=5ab
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:
(1)x2y-y3;
(2) (x-y)2+4(x-y)+4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用简便方法计算:
(1)7.6×201.4+4.3×201.4-1.9×201.4 (2)
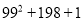
(3)1072 (4)482-472 (5)102×98
相关试题

