【题目】如图,直线l1的解析表达式为y=- ![]() x-1,且l1与x轴交于点D,直线l2经过定点A(2,0),B(-1,3),直线l1与l2交于点C.
x-1,且l1与x轴交于点D,直线l2经过定点A(2,0),B(-1,3),直线l1与l2交于点C.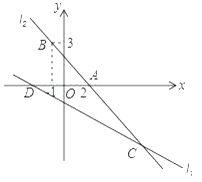
(1)求直线l2的函数关系式;
(2)求△ADC的面积;
(3)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请写出点P的坐标.
参考答案:
【答案】
(1)解:设l2的函数关系式为:y=kx+b,
∵直线过A(2,0),B(-1,3),
∴ ![]() ,解得:
,解得: ![]() ,
,
∴l2的函数关系式为:y=-x+2
(2)解:∵l1的解析表达式为y=- ![]() x-1,
x-1,
∴D点坐标是(-2,0),
∵直线l1与l2交于点C.
∴ 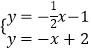 ,解得
,解得 ![]() ,
,
∴C(6,-4),
△ADC的面积为: ![]() ×AD×4=
×AD×4= ![]() ×4×4=8
×4×4=8
(3)解:∵△ADP与△ADC的面积相等,
∴△ADP的面积为8,
∵AD长是4,
∴P点纵坐标是4,
再根据P在l2上,则4=-x+2,解得:x=-2,
故P点坐标为:(-2,4)
【解析】(1)用待定系数法求出直线l2的函数关系式;
(2)先求出D点的坐标,然后解直线l1与l2的解析式组成的方程组,求出C点的坐标,然后利用面积公式计算出△ADC的面积;
(3)根据△ADP与△ADC的面积相等,得出AD的长,从而得出P点纵坐标是4,把P点的纵坐标代入l2得解析式,求出P点的横坐标,从而得出P点的坐标。
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】利群商厦对销量较大的A、B、C三种品牌的纯牛奶进行了问卷调查,共发放问卷300份(问卷由单选和多选题组成),对收回的265份问卷进行了整理,部分数据如下:
(1)最近一次购买各品牌纯牛奶用户比例如图:
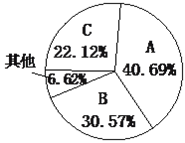
(2)用户对各品牌纯牛奶满意情况汇总如下表:
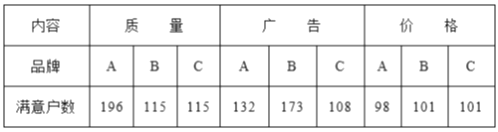
结合上述信息回答下列问题:
①A品牌牛奶的主要竞争优势是什么?请简要说明理由.
②广告对用户选择品牌有影响吗?请简要说明理由.
③你对厂家C有何建议?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果我们想用统计图清楚地描述2014年世界人口分布比例情况,那么应选择的是 .
-
科目: 来源: 题型:
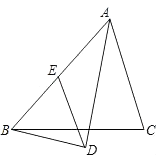
查看答案和解析>>【题目】如图,在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E,若AB=6,求线段DE的长.
-
科目: 来源: 题型:
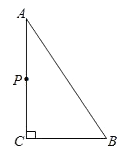
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A-C-B-A运动,设运动时间为t秒(t>0).
(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上,求t的值;
(3)在运动过程中,直接写出当t为何值时,△BCP为等腰三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a3+a4=a7
B.a3a4=a7
C.a3﹣a4=a﹣1
D.a3÷a4=a -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+2x+2m=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若x1,x2是一元二次方程x2+2x+2m=0的两个根,且x12+x22=8,求m的值.
相关试题

