【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2)。
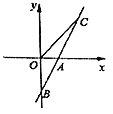
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△AOC =2,求点C的坐标。
参考答案:
【答案】(1)y=2x-2;(2)C(2,2);
【解析】
(1)根据一次函数解析式y=kx+b,再将点(1,0)和点(0,-2)代入可得方程组,解出即可得到k和b的值,即得到解析式.(2)设C点的坐标为(x,y)根据图像可知三角形ABC的面积等于=2,求出C点的横坐标,再代入一次函数AB解析式求出y值即可.
(1)设直线AB的解析式为y=kx+b(k≠0).
∵直线AB过点A(1,0)、点B(0,2),
∴k+b=0 b=2,
解得k=2 b=2,
∴直线AB的解析式为y=2x2.
(2)设点C的坐标为(x,y),
∵S△OBC=2,
∴![]() 2x=2,
2x=2,
解得x=2,
∵直线AB的解析式为y=2x2,
∴当x=2时,y=2×22=2,
∴点C的坐标是(2,2).
-
科目: 来源: 题型:
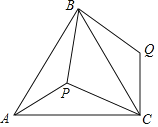
查看答案和解析>>【题目】如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后得到△P′AB.
(1)求点P与点P′之间的距离;
(2)求∠APB的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
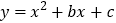 .
.(1)当顶点坐标为
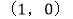 时,求抛物线的解析式;
时,求抛物线的解析式;(2)当
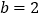 时,
时,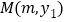 ,
,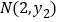 是抛物线图象上的两点,且
是抛物线图象上的两点,且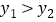 ,求实数
,求实数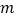 的取值范围;
的取值范围;(3)若抛物线上的点
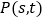 ,满足
,满足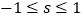 时,
时,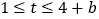 ,求
,求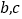 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)的图象交x轴于A(﹣2,0)和点B,交y轴负半轴于点C,抛物线对称轴为x=﹣
 ,下列结论中,错误的结论是( )
,下列结论中,错误的结论是( )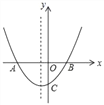
A. abc>0
B. 方程ax2+bx+c=0的解是x1=﹣2,x2=1
C. b2﹣4ac>0
D. a=b
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 相交于
相交于 ,
, 平分
平分 ,给出下列结论:①当
,给出下列结论:①当 时,
时, ;②
;② 为
为 的平分线;③与
的平分线;③与 相等的角有三个;④
相等的角有三个;④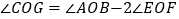 。其中正确的结论有( )
。其中正确的结论有( )
A.
 个B.
个B.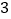 个C.
个C. 个D.
个D. 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式
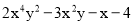 ,次数是b,3a与b互为相反数,在数轴上,点A表示数a,点B表示数b.
,次数是b,3a与b互为相反数,在数轴上,点A表示数a,点B表示数b. 数轴上A、B之间的距离记作
数轴上A、B之间的距离记作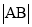 ,定义:
,定义: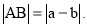 设点C在数轴上对应的数为x,当
设点C在数轴上对应的数为x,当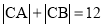 时,直接写出x的值.
时,直接写出x的值. 有一动点P从点A出发第一次向左运动1个单位长度,然后在新的位置第二次运动,向右运动2个单位长度,在此位置第三次运动,向左运动3个单位长度
有一动点P从点A出发第一次向左运动1个单位长度,然后在新的位置第二次运动,向右运动2个单位长度,在此位置第三次运动,向左运动3个单位长度 按照如此规律不断地左右运动,当运动了2019次时,求点P所对应的有理数.
按照如此规律不断地左右运动,当运动了2019次时,求点P所对应的有理数.
 若小蚂蚁甲从点A处以1个单位长度
若小蚂蚁甲从点A处以1个单位长度 秒的速度向左运动,同时小蚂蚁乙从点B处以2单位长度
秒的速度向左运动,同时小蚂蚁乙从点B处以2单位长度 秒的速度也向左运动,一同学观察两只小蚂蚁运动,在它们刚开始运动时,在原点O处放置一颗饭粒,乙在碰到饭粒后立即背着饭粒以原来的速度向相反的方向运动,设运动的时间为t秒,求甲、乙两只小蚂蚁到原点的距离相等时所对应的时间t.
秒的速度也向左运动,一同学观察两只小蚂蚁运动,在它们刚开始运动时,在原点O处放置一颗饭粒,乙在碰到饭粒后立即背着饭粒以原来的速度向相反的方向运动,设运动的时间为t秒,求甲、乙两只小蚂蚁到原点的距离相等时所对应的时间t. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D、E、F分别是边AB、AC、BC的中点,且BC=2AF。
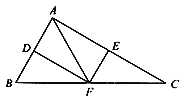
(1)求证:四边形ADEF为矩形;
(2)若∠C=30°、AF=2,写出矩形ADEF的周长。
相关试题

