【题目】已知抛物线![]() .
.
(1)当顶点坐标为![]() 时,求抛物线的解析式;
时,求抛物线的解析式;
(2)当![]() 时,
时,![]() ,
,![]() 是抛物线图象上的两点,且
是抛物线图象上的两点,且![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)若抛物线上的点![]() ,满足
,满足![]() 时,
时,![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() 或
或![]() ;(3)
;(3) ![]() 或
或![]()
【解析】分析:(1)利用抛物线的顶点坐标公式即可得出结论;
(2)先确定出抛物线对称轴x=﹣1,进而得出点Q的坐标,即可得出结论;
(3)分三种情况利用抛物线的增减性建立方程组即可得出结论.
详解:(1)由已知得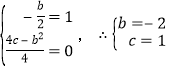 ,
,
∴抛物线的解析式为 y=x2﹣2x+1;
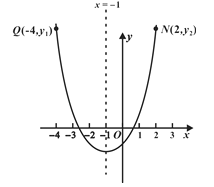
(2)当b=2时,y=x2+2x+c, ∴对称轴直线x=﹣1.
由图取抛物线上点Q,使Q与N关于对称轴x=﹣1对称,由N(2,y2)得Q(﹣4,y2).
又∵M(m,y1)在抛物线图象上的点,且y1>y2,由函数增减性得:m<﹣4或m>2;
(3)分三种情况:
①当﹣![]() <﹣1,即b>2时,函数值y随x的增大而增大,依题意有:
<﹣1,即b>2时,函数值y随x的增大而增大,依题意有:![]()
②当﹣1≤﹣![]() ≤1,即﹣2≤b≤2时,x=﹣
≤1,即﹣2≤b≤2时,x=﹣![]() 时,函数值y取最小值,分两种情况讨论:
时,函数值y取最小值,分两种情况讨论:
(ⅰ)若0≤﹣![]() ≤1,即﹣2≤b≤0时,依题意有:
≤1,即﹣2≤b≤0时,依题意有:
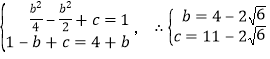 或
或![]() (舍去)
(舍去)
(ⅱ)若﹣1≤﹣![]() ≤0,即0≤b≤2时,依题意有
≤0,即0≤b≤2时,依题意有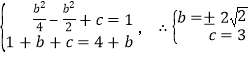 (舍去)
(舍去)
③当﹣![]() >1,即b<﹣
>1,即b<﹣![]() (舍去)
(舍去)
综上所述:![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年4月29日至2019年10月7日,2019年中国北京世界园艺博览会(简称北京世园会)在中国北京市延庆区举行,展期162天.这是继云南昆明后第二个获得国际园艺生产者协会批准及国际展览局认证授权举办的A1级国际园艺博览会.北京世园会门票种类分为平日票、指定日票、三次票等票种,同时按销售对象分为普通票、优惠票和团队票(学生享受优惠票,15人以上可以享受团体票).指定日包括开园日、“五一”假期、端午节假期、中秋节假期、“十一”假期这些日期,其余时间为平日;三次票是指除指定日外,同一持票人在展会期间可以任选三天入园的票种. 具体如下表:
平日票价(元/张)
指定日票价(元/张)
三次票(元/张)
普通票
120
160
300
优惠票
80
100
小明,小亮两家共10人打算一起参观北京世园会(10人均需购票).
(1)若他们端午节去北京世园会参观购买门票共用去1360元,问买了普通票和优惠票各几张?
(2)如果他们平日去北京世园会参观,且购买门票的费用不超过2000元,那么在保证游玩的前提下最多可以买几张三次票?共有几种买票方案?分别是什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在方格纸中,有两条线段AB,BC利用方格纸完成以下操作(保留作图痕迹):
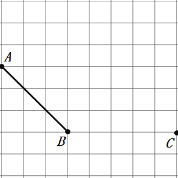
(1)过点A作BC的平行线;
(2)过点C作AB的平行线,与(1)中的平行线交于点D;
(3)过点B作AB的垂线,与(1)中的平行线交于点F.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后得到△P′AB.
(1)求点P与点P′之间的距离;
(2)求∠APB的大小.
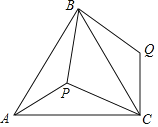
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)的图象交x轴于A(﹣2,0)和点B,交y轴负半轴于点C,抛物线对称轴为x=﹣
 ,下列结论中,错误的结论是( )
,下列结论中,错误的结论是( )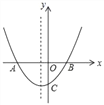
A. abc>0
B. 方程ax2+bx+c=0的解是x1=﹣2,x2=1
C. b2﹣4ac>0
D. a=b
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2)。
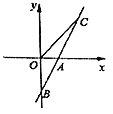
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△AOC =2,求点C的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 相交于
相交于 ,
, 平分
平分 ,给出下列结论:①当
,给出下列结论:①当 时,
时, ;②
;② 为
为 的平分线;③与
的平分线;③与 相等的角有三个;④
相等的角有三个;④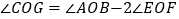 。其中正确的结论有( )
。其中正确的结论有( )
A.
 个B.
个B.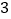 个C.
个C. 个D.
个D. 个
个
相关试题

