【题目】如图，已知B、C、E三点在同一条直线上，△ABC与△DCE都是等边三角形.其中线段BD交AC于点G，线段AE交CD于点F.

求证：（1）△ACE≌△BCD；（2）△GFC是等边三角形.

参考答案：

【答案】（1）证明见解析；（2）证明见解析.

【解析】试题分析：1）利用等边三角形的性质得出条件，可证明：△ACE≌△BCD；

（2）利用△ACE≌△BCD得出∠CBG=∠CAF，再运用平角定义得出∠BCG=∠ACF进而得出△BCG≌△ACF,因此CG=CF，再由∠ACF=60°根据“有一个角是60°的三角形是等边三角形可得△GFC是等边三角形．

试题解析：证明：（1）∵△ABC和△CDE都是等边三角形，

∴∠BCA=∠DCE=60°，BC=AC=AB，EC=CD=ED，

∴∠BCD=∠ACE，

在△BCD和△ACE中，

,

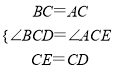∴△ACE≌△BCD；

（2）∵△BCD≌△ACE，

∴∠CBG=∠CAF．

∵∠ACB=∠DCE=60°，

∴∠ACF=60°．

∴∠BCG=∠ACF，

在△BCG和△ACF中，

，

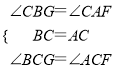∴△BCG≌△ACF（ASA），

∴CG=CF；

∵∠ACF=60°，

∴△GFC是等边三角形．

关闭