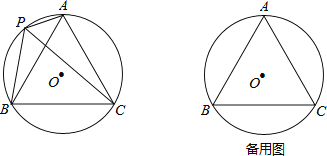
【题目】如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)判断△ABC的形状: ;
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;
(3)当点P位于![]() 的什么位置时,四边形APBC的面积最大?求出最大面积.
的什么位置时,四边形APBC的面积最大?求出最大面积.
参考答案:
【答案】(1)、等边三角形;(2)、CP=BP+AP;证明过程见解析;(3)、当点P为![]() 的中点时,四边形APBC的面积最大,最大值为
的中点时,四边形APBC的面积最大,最大值为![]() .
.
【解析】
试题分析:(1)、根据三角形的判定得出等边三角形;(2)、在PC上截取PD=AP,得出△APD是等边三角形,然后证明△APB和△ADC全等,从而得出BP=CD,然后得出答案;(3)、将四边形的面积转化成△ABP和△ABC的面积之和,然后根据两个三角形同底,要使面积最大,则就需要满足高最大,则当CP是直径时最大.
试题解析:(1)、△ABC是等边三角形
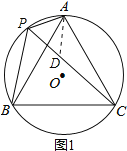
(2)、在PC上截取PD=AP,如图1, 又∵∠APC=60°,∴△APD是等边三角形,
∴AD=AP=PD,∠ADP=60°,即∠ADC=120°. 又∵∠APB=∠APC+∠BPC=120°,∴∠ADC=∠APB,
在△APB和△ADC中,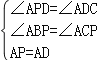 ,∴△APB≌△ADC(AAS), ∴BP=CD,又∵PD=AP, ∴CP=BP+AP
,∴△APB≌△ADC(AAS), ∴BP=CD,又∵PD=AP, ∴CP=BP+AP
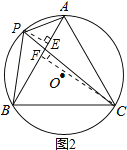
(3)、当点P为![]() 的中点时,四边形APBC的面积最大.
的中点时,四边形APBC的面积最大.
理由如下,如图2,过点P作PE⊥AB,垂足为E. 过点C作CF⊥AB,垂足为F.
∵S△APE=![]() ABPE,S△ABC=
ABPE,S△ABC=![]() ABCF,∴S四边形APBC=
ABCF,∴S四边形APBC=![]() AB(PE+CF),
AB(PE+CF),
当点P为![]() 的中点时,PE+CF=PC,PC为⊙O的直径, ∴此时四边形APBC的面积最大.又∵⊙O的半径为1,
的中点时,PE+CF=PC,PC为⊙O的直径, ∴此时四边形APBC的面积最大.又∵⊙O的半径为1,
∴其内接正三角形的边长AB=![]() , ∴S四边形APBC=
, ∴S四边形APBC=![]() ×2×
×2×![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①“掷一枚质地均匀的骰子两次,两次向上的点数都是6”是随机事件;②小概率事件一定不会发生.( )
A.只有①正确B.只有②正确C.①②都正确D.①②都错误
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,∠B=32°,∠C =48°,AD⊥BC于点D,AE平分∠BAC交BC于点E,DF⊥AE于点F,求∠ADF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:4x4x2﹣(﹣2x2)3﹣3x8÷x2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的周长.
(2)问t为何值时,△BCP为等腰三角形?(要有必要的过程)

-
科目: 来源: 题型:
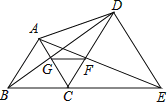
查看答案和解析>>【题目】如图,已知B、C、E三点在同一条直线上,△ABC与△DCE都是等边三角形,其中线段BD交AC于点G,线段AE交CD于点F,求证:
(1)△ACE≌△BCD; (2)
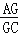 =
=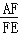 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程(m+1)x2+2mx﹣3=0是一元二次方程,则m的取值是( )
A.任意实数B.m≠1C.m≠﹣1D.m>1
相关试题

