【题目】已知,如图,![]() 、
、![]() 、
、![]() 分别为数轴上的三个点,
分别为数轴上的三个点,![]() 点对应的数为60,
点对应的数为60,![]() 点在
点在![]() 点的左侧,并且与
点的左侧,并且与![]() 点的距离为30,
点的距离为30,![]() 点在
点在![]() 点左侧,
点左侧,![]() 点到
点到![]() 距离是
距离是![]() 点到
点到![]() 点距离的4倍.
点距离的4倍.
![]()
(1)求出数轴上![]() 点对应的数及
点对应的数及![]() 的距离.
的距离.
(2)点![]() 从
从![]() 点出发,以3单位/秒的速度项终点
点出发,以3单位/秒的速度项终点![]() 运动,运动时间为
运动,运动时间为![]() 秒.
秒.
①点![]() 点在
点在![]() 之间运动时,则
之间运动时,则![]() _______.(用含
_______.(用含![]() 的代数式表示)
的代数式表示)
②![]() 点在
点在![]() 点向
点向![]() 点运动过程中,何时
点运动过程中,何时![]() 、
、![]() 、
、![]() 三点中其中一个点是另外两个点的中点?求出相应的时间
三点中其中一个点是另外两个点的中点?求出相应的时间![]() .
.
③当![]() 点运动到
点运动到![]() 点时,另一点
点时,另一点![]() 以5单位/秒速度从
以5单位/秒速度从![]() 点出发,也向
点出发,也向![]() 点运动,点
点运动,点![]() 到达
到达![]() 点后立即原速返回到
点后立即原速返回到![]() 点,那么
点,那么![]() 点在往返过程中与
点在往返过程中与![]() 点相遇几次?直接写出相遇是
点相遇几次?直接写出相遇是![]() 点在数轴上对应的数.
点在数轴上对应的数.
参考答案:
【答案】(1)![]() 点对应的数为30;AC=120;(2)①
点对应的数为30;AC=120;(2)①![]() ;②
;②![]() 的值为5或20;③相遇2次;
的值为5或20;③相遇2次;![]() 点在数轴上对应的数为-15或
点在数轴上对应的数为-15或![]() .
.
【解析】
(1)根据A点对应的数为60,B点在A点的左侧,AB=30求出B点对应的数,根据AC=4AB求出AC的距离;
(2)①当P点在AB之间运动时,根据路程=速度×时间求出AP=3t,根据BP=AB-AP求解;
②分P点是AB的中点和B点是AP的中点两种情况进行讨论即可;
③根据P、Q两点的运动速度与方向可知Q点在往返过程中与P点相遇2次,设Q点在往返过程中经过x秒与P点相遇,第一次相遇是点Q从A点出发,向C点运动的途中,根据AQ-BP=AB列出方程;第二次相遇是点Q到达C点后返回到A点的途中,根据CQ+BP=BC列出方程,进而求出P点在数轴上的对应的数.
解(1)![]()
![]() 点对应的数为60,
点对应的数为60,![]() ,点在
,点在![]() 点的左侧,并且与
点的左侧,并且与![]() 点的距离为30,
点的距离为30,
![]()
![]() 点对应的数为
点对应的数为![]() ;
;
![]()
![]() 点到
点到![]() 点距离是
点距离是![]() ,点到
,点到![]() 点距离的4倍,
点距离的4倍,
![]()
![]() ;
;
(2)①当![]() 点在
点在![]() 之间运动时,
之间运动时,
![]() ,
,
![]() .
.
故答案为![]() ;
;
②当![]() 点是
点是![]() 、
、![]() 两点的中点时,
两点的中点时,![]() ,
,
![]() ,解得
,解得![]() ;
;
当![]() 点是
点是![]() 两点的中点时,
两点的中点时,![]() ,
,
![]() ,解得
,解得![]() .
.
故所求时间![]() 的值为5或20;
的值为5或20;
③相遇2次.
设![]() 点在往返过程中经过
点在往返过程中经过![]() 秒与
秒与![]() 点相遇.
点相遇.
第一次相遇是点![]() 从
从![]() 出发,向
出发,向![]() 点运动的途中.
点运动的途中.
![]() ,
,
![]() ,
,
解得![]() ,
,
此时![]() 点在数轴上对应的数是:
点在数轴上对应的数是:![]() ;
;
第二次相遇是![]() 到达
到达![]() 点后返回到
点后返回到![]() 点的途中.
点的途中.
![]() ,
,
![]() ,
,
解得![]() ,
,
此时![]() 点在数轴上对应的数是:
点在数轴上对应的数是:![]() .
.
综上,相遇时![]() 点在数轴上对应的数为-15或
点在数轴上对应的数为-15或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,
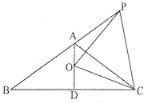
(1)求∠APO+∠DCO的度数;
(2)求证:点P在OC的垂直平分线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, ,小聪同学利用直尺和圆规完成了如下操作:
,小聪同学利用直尺和圆规完成了如下操作:①作
 的平分线
的平分线 交
交 于点
于点 ;
;②作边
 的垂直平分线
的垂直平分线 ,
, 与
与 相交于点
相交于点 ;
;③连接
 ,
,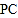 .
.请你观察图形解答下列问题:

(1)线段
 ,
, ,
,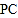 之间的数量关系是________;
之间的数量关系是________;(2)若
 ,求
,求 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】从2开始的连续偶数相加,它们和的情况如下表:
加数的个数(n)
和(S)
1
2=1×2
2
2+4=6=2×3
3
2+4+6=12=3×4
4
2+4+6+8=20=4×5
5
2+4+6+8+10=30=5×6
…
…
(1)根据表中的规律,直接写出2+4+6+8+10+12+14=________
(2)根据表中的规律猜想:S=2+4+6+8+…+2n=___________(用n的代数式表示);
(3)利用上题中的公式计算102+104+106+…+200的值(要求写出计算过程).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,Rt△BAP中,∠BAP=90°,已知∠CBO=∠ABP,BP交AC于点O,E为AC上一点,且AE=OC.
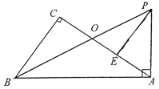
(1)求证:AP=AO;
(2)求证:PE⊥AO.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
 的一元二次方程
的一元二次方程 .
.(1)试证明:无论
 取何值此方程总有两个实数根;
取何值此方程总有两个实数根;(2)若原方程的两根
 ,
, 满足
满足 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进的乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,购进这两种玩具的总资金超过960元但不超过1000元,求商场有哪几种具体的进货方案?最多可以购进乙种玩具多少件?
相关试题

