Question

【题目】在平面直角坐标系中，O为原点，点A（﹣2，0），点B（0，2），点E，点F分别为OA，OB的中点．若正方形OEDF绕点O顺时针旋转，得正方形OE′D′F′，记旋转角为α．

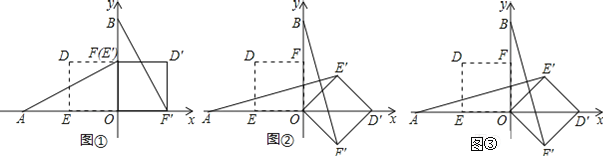
（1）如图②，当α=135°时，求AE′，BF′的长；

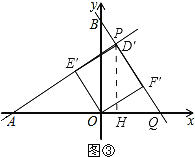
（2）如图③，当0°﹤α﹤180°时， AE′和BF′有什么位置关系；

（3）若直线AE′与直线BF′相交于点P，求点P的纵坐标的最大值（直接写出结果即可）．

Answer 1

【答案】（1）AE′,BF′的长都等于；

（2）AE′⊥BF′；

（3）点P的纵坐标的最大值为+12.

【解析】试题分析：（1）利用勾股定理即可求出AE′，BF′的长（2）运用全等三角形的判定与性质、三角形的外角性质就可解决问题．（3）首先找到使点P的纵坐标最大时点P的位置（点P与点D′重合时），然后运用勾股定理及30°角所对的直角边等于斜边的一半等知识即可求出点P的纵坐标的最大值．

试题解析：(Ⅰ)当α=90时,点E′与点F重合，如图①。

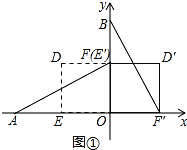
∵点A(2,0)点B(0,2)，

∴OA=OB=2.

∵点E，点F分别为OA，OB的中点，

∴OE=OF=1

∵正方形OE′D′F′是正方形OEDF绕点O顺时针旋转90°得到的，

∴OE′=OE=1,OF′=OF=1.

在Rt△AE′O中，

AE′===.

在Rt△BOF′中，

BF′===.

∴AE′,BF′的长都等于.

(Ⅱ)当α=135°时,如图②。

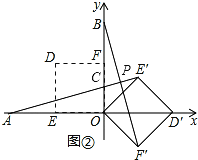
∵正方形OE′D′F′是由正方形OEDF绕点O顺时针旋转135°所得，

∴∠AOE′=∠BOF′=135°.

在△AOE′和△BOF′中，

，

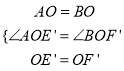∴△AOE′≌△BOF′(SAS).

∴AE′=BF′,且∠OAE′=∠OBF′.

∵∠ACB=∠CAO+∠AOC=∠CBP+∠CPB，∠CAO=∠CBP，

∴∠CPB=∠AOC=90°

∴AE′⊥BF′.

(Ⅲ)∵∠BPA=∠BOA=90°，

∴点P、B. A.O四点共圆，

∴当点P在劣弧OB上运动时，点P的纵坐标随着∠PAO的增大而增大。

∵OE′=1，

∴点E′在以点O为圆心,1为半径的圆O上运动,

∴当AP与O相切时,∠E′AO(即∠PAO)最大，

此时∠AE′O=90°,点D′与点P重合，点P的纵坐标达到最大。

过点P作PH⊥x轴，垂足为H，如图③所示。

∵∠AE′O=90°,E′O=1，AO=2，

∴∠E′AO=30°,AE′=.

∴AP=+1.

∵∠AHP=90°,∠PAH=30°，

∴PH=AP=.

∴点P的纵坐标的最大值为.