【题目】按照有关规定:距高铁轨道 200米以内的区域内不宜临路新建学校、医院、敬老院和集中住宅区等噪声敏感建筑物.
如图是一个小区平面示意图,矩形ABEF为一新建小区,直线MN为高铁轨道,C、D是直线MN上的两点,点C、A、B在一直线上,且DA⊥CA,∠ACD=30°.小王看中了①号楼A单元的一套住宅,与售楼人员的对话如下: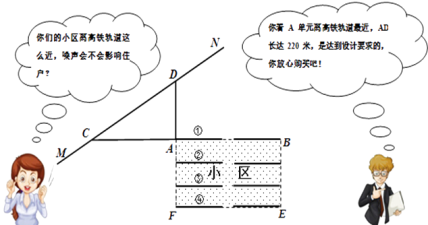
(1)小王心中一算,发现售楼人员的话不可信,请你用所学的数学知识说明理由;
(2)若一列长度为228米的高铁以252千米/小时的速度通过时,则A单元用户受到影响时间有多长?
(温馨提示: ![]() ≈1.4,
≈1.4, ![]() ≈1.7,
≈1.7, ![]() ≈6.1)
≈6.1)
参考答案:
【答案】
(1)
解:作过点A作AG⊥MN,垂足为G,
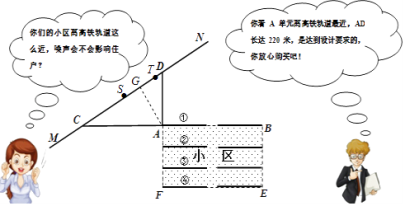
∵∠ACD=30°,DA⊥CA,
∴∠ADC=60°,
∵AD=220米,
∴AG=ADsin60°=110 ![]() ≈187<200,
≈187<200,
∴A单元用户会受到影响,售楼人员的说法不可信.
(2)
解:在MN上找到点S、T,使得AS=AT=200米
∴GT=GS= ![]() =10
=10 ![]() 米
米
∴ST=2GT=20 ![]() ≈122米
≈122米
又∵速度V= ![]() =70(米/秒)
=70(米/秒)
∴时间t= ![]() =5秒,即受影响的时间为5秒.
=5秒,即受影响的时间为5秒.
【解析】(1)作过点A作AG⊥MN,垂足为G,根据三角函数可求AG的长,再与200米比较大小即可求解;(2)在MN上找到点S、T,使得AS=AT=200米,根据勾股定理可求GT,根据三角函数可求ST,依此可求速度,进一步得到A单元用户受到影响的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是边长为a的正方形,点G、E分别是边AB、BC的中点,∠AEF=90°,且EF交正方形外角的平方线CF于点F.

(1)证明:△AGE≌△ECF;
(2)求△AEF的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰Rt△ABC和等腰Rt△AED中,∠ACB=∠AED=90°,且AD=AC.
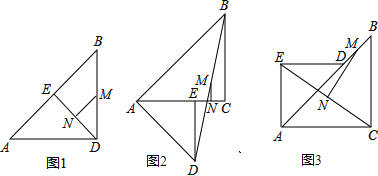
(1)发现:如图1,当点E在AB上且点C和点D重合时,若点M、N分别是DB、EC的中点,则MN与EC的位置关系是 ,MN与EC的数量关系是 .
(2)探究:若把(1)小题中的△AED绕点A顺时针旋转45°得到的图2,连接BD和EC,并连接DB、EC的中点M、N,则MN与EC的位置关系和数量关系仍然能成立吗?若成立,请给予证明,若不成立,请说明理由.
(3)若把(1)小题中的△AED绕点A逆时针旋转45°得到的图3,连接BD和EC,并连接DB、EC的中点M、N,则MN与EC的位置关系和数量关系仍然能成立吗?若成立,请给予证明,若不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在⊙O中,
 =
= 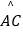 ,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC.
,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC. 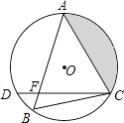
(1)求证:AC2=ABAF;
(2)若⊙O的半径长为2cm,∠B=60°,求图中阴影部分面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:销售单价(元)
x
销售量y(件)
销售玩具获得利润w(元)
(2)在(1)问条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元.
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的对角线AC与BD互相垂直,若AB=3,BC=4,CD=5,则AD的长为( )
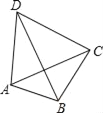
A. 3
 B. 4
B. 4 C. 2
C. 2 D. 4
D. 4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图正方形ABCD边长为10,AG=CH=8,BG=DH=6,连接GH,则线段GH的长为( )
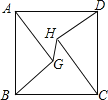
A.
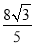 B.
B. 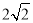 C.
C. 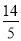 D. 10-5
D. 10-5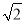
相关试题

