【题目】某农科所甲、乙试验田各有水稻3万个,为了考察水稻穗长的情况,于同一天在这两块试验田里分别随机抽取了![]() 个稻穗进行测量,获得了它们的长度
个稻穗进行测量,获得了它们的长度![]() (单位:cm),并对数据(穗长)进行了整理、描述和分析.下面给出了部分信息.
(单位:cm),并对数据(穗长)进行了整理、描述和分析.下面给出了部分信息.
a.甲试验田穗长的频数分布统计表如下表所示(不完整):
甲试验田穗长频数分布表
分组/ | 频数 | 频率 |
| 4 | 0.08 |
| 9 | 0.18 |
|
| |
| 11 | 0.22 |
|
| 0.20 |
| 2 | |
合计 | 50 | 1.00 |
b.乙试验田穗长的频数分布直方图如图所示:
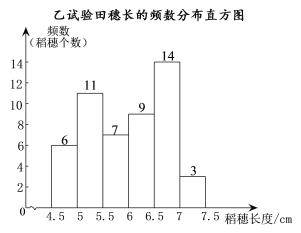
c.乙试验田穗长在![]() 这一组的是:
这一组的是:
6.3 6.4 6.3 6.3 6.2 6.2 6.1 6.2 6.4
d.甲、乙试验田穗长的平均数、中位数、众数、方差如下(表2):
试验田 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 5.924 | 5.8 | 5.8 | 0.454 |
乙 | 5.924 |
| 6.5 | 0.608 |
根据以上信息,回答下列问题:
(1)表中![]() 的值为 ,
的值为 ,![]() 的值为 ;
的值为 ;
(2)表中![]() 的值为 ;
的值为 ;
(3)在此次考察中,稻穗生长(长度)较稳定的试验田是 ;
A.甲 B.乙 C.无法推断
(4)若穗长在![]() 范围内的稻穗为“良好”,请估计甲试验田所有“良好”的水稻约为 万个.
范围内的稻穗为“良好”,请估计甲试验田所有“良好”的水稻约为 万个.
参考答案:
【答案】(1)![]() ;
;![]() ;(2)
;(2)![]() ;(3)A;A;(4)
;(3)A;A;(4)![]() .
.
【解析】
(1)根据“频率=![]() ”求解即可;
”求解即可;
(2)根据中位数的定义求解即可;
(3)由于平均数相同,比较方差大小即可得出结论;
(4)先求出样本中“良好”所占百分数,再乘以总数即可.
(1)m=50×0.20=10;
2÷50=0.04,
n=1-0.04-0.20-0.22-0.18-0.08=0.28.
(2)样本共有50个数据,按大小顺序排列第25、26个数是最中间的两个数,
而第25、26个数是6.1和6.2,
因此,中位数是![]() (cm).
(cm).
(3)∵甲试验田穗长的方差小于乙试验田穗长的方差,
故选A.
(4)穗长在![]() 范围内的稻穗数为50-(4+9+2)=35,
范围内的稻穗数为50-(4+9+2)=35,
30000×![]() =21000=2.1万.
=21000=2.1万.
所以,甲试验田所有“良好”的水稻约为2.1万个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 的正方形网格中,每个小正方形的边长均为
的正方形网格中,每个小正方形的边长均为 ,每个小正方形的顶点叫做格点.
,每个小正方形的顶点叫做格点. 的顶点都在格点上.按照要求完成下列画图(只在此
的顶点都在格点上.按照要求完成下列画图(只在此 的网格中完成且所画各点都是格点,所画的点可以与已知点重合).
的网格中完成且所画各点都是格点,所画的点可以与已知点重合).
(1)将
 绕点
绕点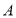 逆时针旋转
逆时针旋转 ,得到
,得到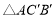 ;
;(2)画出所有点
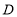 ,使得以
,使得以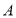 ,
, ,
,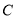 ,
,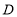 为顶点的四边形是平行四边形;
为顶点的四边形是平行四边形;(3)画出一个与
 相似(但不全等)的三角形
相似(但不全等)的三角形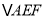 ,且
,且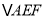 与
与 有公共点
有公共点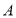 (画出一个三角形即可).
(画出一个三角形即可). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,二次函数y=ax2+bx的图象过点A(﹣1,3),顶点B的横坐标为1.

(1)求这个二次函数的表达式;
(2)点P在该二次函数的图象上,点Q在x轴上,若以A、B、P、Q为顶点的四边形是平行四边形,求点P的坐标;
(3)如图3,一次函数y=kx(k>0)的图象与该二次函数的图象交于O、C两点,点T为该二次函数图象上位于直线OC下方的动点,过点T作直线TM⊥OC,垂足为点M,且M在线段OC上(不与O、C重合),过点T作直线TN∥y轴交OC于点N.若在点T运动的过程中,
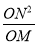 为常数,试确定k的值.
为常数,试确定k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象如图所示,给出下列说法:①ac>0;②当x>1时,函数y随x的增大而增大;③a+b+c=0;④2a+b=0;⑤当y>0时,﹣1<x<3.其中,正确的说法有( )个
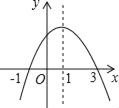
A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲地的海拔高度是
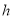 米,乙地的海拔高度比甲地海拔高度的
米,乙地的海拔高度比甲地海拔高度的 倍多
倍多 米,丙地的海拔高度比甲地海拔高度的
米,丙地的海拔高度比甲地海拔高度的 倍少
倍少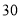 米.
米.(1) 三地的海拔高度和一共是多少米?;
(2) 乙地的海拔高度比丙地的海拔高度高多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形
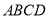 中,点
中,点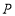 是直线
是直线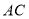 上的一个动点,连接
上的一个动点,连接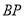 ,将线段
,将线段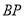 绕点
绕点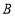 顺时针旋转
顺时针旋转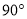 得到线段
得到线段 ,连接
,连接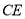 .
.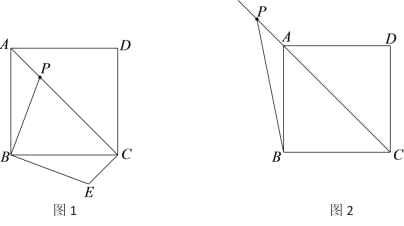
(1)如图1,若点
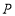 在线段
在线段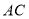 上,
上,①直接写出
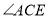 的度数为 °;
的度数为 °;②求证:
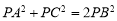 ;
;(2)如图2,若点
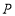 在
在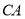 的延长线上,
的延长线上,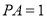 ,
,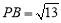 ,
,①依题意补全图2;
②直接写出线段
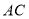 的长度为 .
的长度为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】点
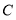 在线段
在线段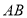 上,
上,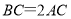 .
.(1) 如图1,
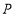 ,
,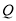 两点同时从
两点同时从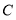 ,
,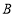 出发,分别以
出发,分别以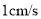 ,
,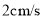 的速度沿直线
的速度沿直线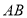 向左运动;
向左运动;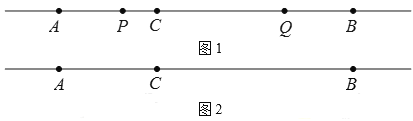
①在
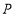 还未到达
还未到达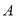 点时,
点时,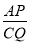 的值为 ;
的值为 ;②当
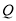 在
在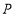 右侧时(点
右侧时(点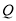 与
与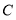 不重合),取
不重合),取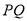 中点
中点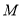 ,
,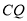 的中点是
的中点是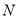 ,求
,求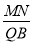 的值;
的值;(2) 若
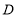 是直线
是直线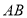 上一点,且
上一点,且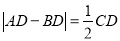 .则
.则 的值为 .
的值为 .
相关试题

