【题目】如图,BD和CD分别平分△ABC的内角∠EBA和外角∠ECA,BD交AC于F,连接AD. 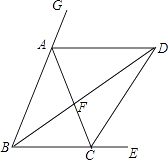
(1)求证:∠BDC= ![]() ∠BAC;
∠BAC;
(2)若AB=AC,请判断△ABD的形状,并证明你的结论;
(3)在(2)的条件下,若AF=BF,求∠EBA的大小.
参考答案:
【答案】
(1)解:∵BD、CD分别平分∠EBA、∠ECA,BD交AC于F,
∴∠BDC+ ![]() ∠ABC=
∠ABC= ![]() ∠ACE,∠BAC+∠ABC=∠ACE,
∠ACE,∠BAC+∠ABC=∠ACE,
∴∠BDC+ ![]() ∠ABC=
∠ABC= ![]() ∠BAC+
∠BAC+ ![]() ∠ABC,
∠ABC,
∴∠BDC= ![]() ∠BAC
∠BAC
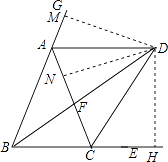
(2)解:△ABD为等腰三角形,证明如下:
作DM⊥BG于M,DN⊥AC于N,DH⊥BE于H
∵BD、CD分别平分∠EBA、∠ECA,
∴DM=DH,DN=DH,
∴DM=DN,
∴AD平分∠CAG,即∠GAD=∠CAD,
∵∠GAD+∠CAD+∠BAC=180°,∠BAC+∠ABC+∠ACB=180°,
∴∠GAD+∠CAD=∠ABC+∠ACB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠GAD=∠ABC,
∴AD∥BC,
∴∠ADB=∠DBC,
又∵∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD,
∴△ABD为等腰三角形
(3)解:∵AF=BF,
∴∠BAF=∠ABF= ![]() ∠ABC,
∠ABC,
∵∠BAF+∠ABC+∠ACB=180°,∠ABC=∠ACB,
∴ ![]() ∠ABC=180°,
∠ABC=180°,
∴∠ABC=72°.
【解析】(1)根据角平分线的定义得到∠BDC+ ![]() ∠ABC=
∠ABC= ![]() ∠ACE,∠BAC+∠ABC=∠ACE,于是得到∠BDC+
∠ACE,∠BAC+∠ABC=∠ACE,于是得到∠BDC+ ![]() ∠ABC=
∠ABC= ![]() ∠BAC+
∠BAC+ ![]() ∠ABC,等量代换即可得到结论;(2)作DM⊥BG于M,DN⊥AC于N,DH⊥BE于H根据角平分线的性质得到DM=DH,DN=DH,等量代换得到DM=DN,根据三角形的内角和得到∠GAD+∠CAD+∠BAC=180°,∠BAC+∠ABC+∠ACB=180°,推出∠GAD+∠CAD=∠ABC+∠ACB,由等腰三角形的性质得到∠ABC=∠ACB,等量代换得到∠GAD=∠ABC,推出AD∥BC,由平行线的性质得到∠ADB=∠DBC,证得∠ABD=∠ADB,即可得到结论;(3)根据等腰三角形的性质得到∠BAF=∠ABF=
∠ABC,等量代换即可得到结论;(2)作DM⊥BG于M,DN⊥AC于N,DH⊥BE于H根据角平分线的性质得到DM=DH,DN=DH,等量代换得到DM=DN,根据三角形的内角和得到∠GAD+∠CAD+∠BAC=180°,∠BAC+∠ABC+∠ACB=180°,推出∠GAD+∠CAD=∠ABC+∠ACB,由等腰三角形的性质得到∠ABC=∠ACB,等量代换得到∠GAD=∠ABC,推出AD∥BC,由平行线的性质得到∠ADB=∠DBC,证得∠ABD=∠ADB,即可得到结论;(3)根据等腰三角形的性质得到∠BAF=∠ABF= ![]() ∠ABC,根据三角形的内角和即可得到结论.
∠ABC,根据三角形的内角和即可得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在从小到大排列的五个整数中,中位数是2,唯一的众数是4,则这五个数和的最大值是( )
A. 11B. 12C. 13D. 14
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:
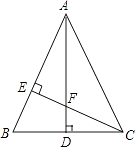
(1)△AEF≌△CEB;
(2)AF=2CD. -
科目: 来源: 题型:
查看答案和解析>>【题目】按要求完成作图,并回答问题;如图在△ABC中:

(1)过点A画BC的垂线,垂足为E;
(2)画∠ABC的平分线,交AC于F;
(3)过E画AB的平行线,交AC于点G;
(4)过点C画AB所在的直线的垂线段,垂足为H. -
科目: 来源: 题型:
查看答案和解析>>【题目】星期天小明去逛商场,他发现商场共有四层,第一层有商品a(a+b)种,第二层有(a+b)2种,第三层有b(a+b)种,第四层有(a-b)2种,则这个商场共有多少种商品?
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用直尺画图:
(1)利用图1中的网格,过P点画直线AB的平行线和垂线.
(2)把图(2)网格中的三条线段通过平移使三条线段AB、CD、EF首尾顺次相接组成一个三角形.
(3)在图(3)的网格中画一个三角形:满足①是直角三角形;②任意两个顶点都不在同一条网格线上;③三角形的顶点都在格点上(即在网格线的交点上).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列分解因式正确的是( )
A.﹣a+a3=﹣a(1+a2)
B.2a﹣4b+2=2(a﹣2b)
C.a2﹣4=(a﹣2)2
D.a2﹣2a+1=(a﹣1)2
相关试题

