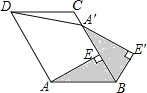
【题目】如图,已知平行四边形ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,∠ADA′=50°,则∠DA′E′的度数为 .
参考答案:
【答案】160°.
【解析】
试题分析:根据平行四边形的性质得∠ABC=∠ADC=60°,AD∥BC,则根据平行线的性质可计算出∠DA′B=130°,接着利用互余计算出∠BAE=30°,然后根据旋转的性质得∠BA′E′=∠BAE=30°,于是可得∠DA′E′=160°.
解:∵四边形ABCD为平行四边形,
∴∠ABC=∠ADC=60°,AD∥BC,
∴∠ADA′+∠DA′B=180°,
∴∠DA′B=180°﹣50°=130°,
∵AE⊥BE,
∴∠BAE=30°,
∵△BAE顺时针旋转,得到△BA′E′,
∴∠BA′E′=∠BAE=30°,
∴∠DA′E′=130°+30°=160°.
故答案为160°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式从左到右的变形,是因式分解的是( )
A. x2﹣9+6x=(x+3)(x﹣3)+6x B. (x+5)(x﹣2)=x2+3x﹣10
C. x2﹣8x+16=(x﹣4)2 D. 6ab=2a3b
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a2+b2=13,ab=6,则a4-2a2b2+b4=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABO在直角坐标系中,AB⊥x轴于点B,AO=10,sin∠AOB=
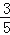 ,反比例函数y=
,反比例函数y=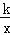 (x>0)的图象经过AO的中点C,且与AB交于点D,则BD= .
(x>0)的图象经过AO的中点C,且与AB交于点D,则BD= .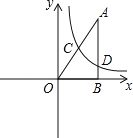
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O中,弦AB=AC,点P是∠BAC所对弧上一动点,连接PB、PA.
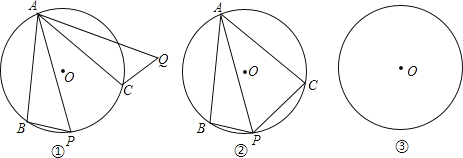
(Ⅰ)如图①,把△ABP绕点A逆时针旋转到△ACQ,求证:点P、C、Q三点在同一直线上.
(Ⅱ)如图②,若∠BAC=60°,试探究PA、PB、PC之间的关系.
(Ⅲ)若∠BAC=120°时,(2)中的结论是否成立?若是,请证明;若不是,请直接写出它们之间的数量关系,不需证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】太阳半径约为696 000千米,数字696 000用科学记数法表示为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx﹣
 ,经过A(﹣1,0),B(5,0)两点.
,经过A(﹣1,0),B(5,0)两点.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
相关试题

