【题目】如图,四边形ABCD是菱形,点G是BC延长线上一点,连接AG,分别交BD、CD于点E、F,连接CE. 
(1)求证:∠DAE=∠DCE;
(2)当AE=2EF时,判断FG与EF有何等量关系?并证明你的结论.
参考答案:
【答案】
(1)证明:∵四边形ABCD是菱形,
∴AD=CD,∠ADE=∠CDB;
在△ADE和△CDE中,
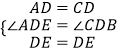
∴△ADE≌△CDE,
∴∠DAE=∠DCE
(2)解:判断FG=3EF.
∵四边形ABCD是菱形,
∴AD∥BC,
∴∠DAE=∠G,
由题意知:△ADE≌△CDE
∴∠DAE=∠DCE,
则∠DCE=∠G,
∵∠CEF=∠GEC,
∴△ECF∽△EGC,
∴ ![]() ,
,
∵△ADE≌△CDE,
∴AE=CE,
∵AE=2EF,
∴ ![]() =
= ![]() ,
,
∴EG=2AE=4EF,
∴FG=EG﹣EF=4EF﹣EF=3EF.

【解析】(1)根据四边形ABCD是菱形可得出△ADE≌△CDE就可证明;(2)根据有两组角对应相等的两个三角形相似得到△CEF∽△GEC,可得EF:EC=CE:GE,又因为△ABE≌△CBE AE=2EF,就能得出FG=3EF.
【考点精析】本题主要考查了菱形的性质和相似三角形的判定与性质的相关知识点,需要掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中考体育测试满分为40分,某校九年级进行了中考体育模拟测试,随机抽取了部分学生的考试成绩进行统计分析,并把分析结果绘制成如下两幅统计图.试根据统计图中提供的数据,回答下列问题:

(1)抽取的样本中,成绩为39分的人数有人;
(2)抽取的样本中,考试成绩的中位数是分,众数是分;
(3)若该校九年级共有500名学生,试根据这次模拟测试成绩估计该校九年级将有多少名学生能得到满分? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,过对角线BD上一点P作EF∥AB,GH∥AD,与各边交点分别为点E,F,G,H,则图中面积相等的平行四边形的对数为( )
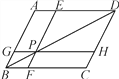
A. 3对 B. 4对 C. 5对 D. 6对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在活动课上,小明和小红合作用一副三角板来测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,他调整自己的位置,设法使得三角板的一条直角边保持水平,且斜边与旗杆顶端M在同一条直线上,测得旗杆顶端M仰角为45°;小红眼睛与地面的距离(CD)是1.5m,用同样的方法测得旗杆顶端M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).求出旗杆MN的高度.(参考数据:
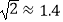 ,
, 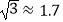 ,结果保留整数.)
,结果保留整数.)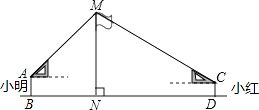
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AB=6,AD=10,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,AG=2.5,则△CEF的周长为

-
科目: 来源: 题型:
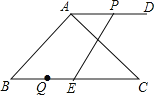
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,∠B=45°,BC=10,过点A作AD∥BC,且点D在点A的右侧.点P从点A出发沿射线AD方向以每秒1个单位的速度运动,同时点Q从点C出发沿射线CB方向以每秒2个单位的速度运动,在线段QC上取点E,使得QE=2,连结PE,设点P的运动时间为t秒.
(1)若PE⊥BC,求BQ的长;
(2)请问是否存在t的值,使以A,B,E,P为顶点的四边形为平行四边形?若存在,求出t的值;若不存在,请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2017次运动后,动点P的坐标是______.

相关试题

