【题目】已知:如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥AC,垂足为K.过D作DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H. 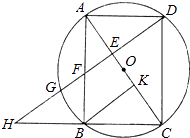
(1)求证:AE=CK;
(2)如果AB=a,AD= ![]() (a为大于零的常数),求BK的长:
(a为大于零的常数),求BK的长:
(3)若F是EG的中点,且DE=6,求⊙O的半径和GH的长.
参考答案:
【答案】
(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,
∴∠DAE=∠BCK,
∵BK⊥AC,DH∥KB,
∴∠BKC=∠AED=90°,
∴△BKC≌△ADE,
∴AE=CK
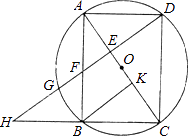
(2)解:∵AB=a,AD= ![]() =BC,
=BC,
∴AC= ![]() =
= ![]() =
= ![]()
![]()
∵BK⊥AC,∠ABC=90°,
∴在Rt△ABC中,由三角形的面积公式得: ![]() AB×BC=
AB×BC= ![]() AC×BK,
AC×BK,
∴a× ![]() a=
a= ![]() a×BK,
a×BK,
∴BK= ![]() a
a
(3)解:DG是圆的弦,又有AE⊥GD得GE=ED,
∵DE=6,
∴GE=6,
又∵F为EG中点,
∴EF= ![]() EG=3,
EG=3,
∵△BKC≌△DEA,
∴BK=DE=6,
∴EF= ![]() BK,且EF∥BK,
BK,且EF∥BK,
∴△AEF∽△AKB,且相似比为1:2,
∴EF为△ABK的中位线,
∴AF=BF,
又∵∠ADF=∠H,∠DAF=∠HBF=90°,
∴△AFD≌△BFH(AAS),
∴HF=DF=3+6=9,
∴GH=6,
∵DH∥KB,BK⊥AC,四边形ABCD为矩形,
∴∠AEF=∠DEA=90°,
∴∠FAE+∠DAE=∠FAE+∠AFE=90°,
∴∠AFE=∠DAE,
∴△AEF∽△DEA,
∴AE:ED=EF:AE,
∴AE2=EFED=3×6=18,
∴AE=3 ![]() ,
,
∵△AED∽△HEC,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴AE= ![]() AC,
AC,
∴AC=9 ![]() ,
,
则AO= ![]() ,
,
故⊙O的半径是 ![]() ,GH的长是6.
,GH的长是6.
【解析】(1)根据ABCD是矩形,求证△BKC≌△ADE即可;(2)根据勾股定理求得AC的长,根据三角形的面积公式得出 ![]() AB×BC=
AB×BC= ![]() AC×BK,代入即可求得BK.(3)根据三角形中位线定理可求出EF,再利用△AFD≌△HBF可求出HF,然后即可求出GH;利用射影定理求出AE,再利△AED∽△HEC求证AE=
AC×BK,代入即可求得BK.(3)根据三角形中位线定理可求出EF,再利用△AFD≌△HBF可求出HF,然后即可求出GH;利用射影定理求出AE,再利△AED∽△HEC求证AE= ![]() AC,然后即可求得AC即可.
AC,然后即可求得AC即可.
【考点精析】掌握三角形中位线定理和垂径定理是解答本题的根本,需要知道连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=
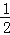 BC,连接CD和EF.
BC,连接CD和EF.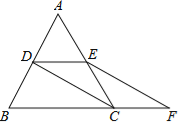
(1)求证:DE=CF;
(2)求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校要在围墙旁建一个长方形的中药材种植实习苗圃,苗圃的一边靠围墙(墙的长度不限),另三边用木栏围成,建成的苗圃为如图所示的长方形ABCD.已知木栏总长为120米,设AB边的长为x米,长方形ABCD的面积为S平方米.
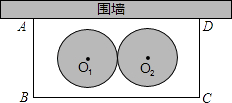
(1)求S与x之间的函数关系式(不要求写出自变量x的取值范围).当x为何值时,S取得最值(请指出是最大值还是最小值)?并求出这个最值;
(2)学校计划将苗圃内药材种植区域设计为如图所示的两个相外切的等圆,其圆心分别为O1和O2 , 且O1到AB、BC、AD的距离与O2到CD、BC、AD的距离都相等,并要求在苗圃内药材种植区域外四周至少要留够0.5米宽的平直路面,以方便同学们参观学习.当(l)中S取得最值时,请问这个设计是否可行?若可行,求出圆的半径;若不可行,请说明理由. -
科目: 来源: 题型:
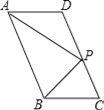
查看答案和解析>>【题目】如图,在ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的周长是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( ).
A.两直线平行,内错角相等
B.过直线外一点有且只有一条直线与已知直线平行
C.同旁内角互补,两直线平行
D.过一点有且只有一条直线垂直于已知直线
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式2x﹣1≤1的解集是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x,y为实数,且|x+2|+(y2﹣2y+1)=0,则(x+y)3的值为____.
相关试题

