【题目】如图,在Rt△ABC中,∠C=90°,∠A=30°.点D是AB中点,点E为边AC上一点,连接CD,DE,以DE为边在DE的左侧作等边三角形DEF,连接BF.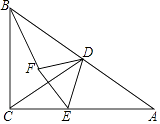
(1)△BCD的形状为;
(2)随着点E位置的变化,∠DBF的度数是否变化?并结合图说明你的理由;
(3)当点F落在边AC上时,若AC=6,请直接写出DE的长.
参考答案:
【答案】
(1)等边三角形
(2)解:∠DBF的度数不变,理由如下:
∵∠ACB=90°,点D是AB中点,
∴CD= ![]() AB=AD,
AB=AD,
∴∠ECD=30°.
∵△BDC为等边三角形,
∴BD=DC,∠BDC=60°.
又∵△DEF为等边三角形,
∴DF=DE,∠FDE=60°,
∴∠BDF+∠FDC=∠EDC+∠FDC=60°,
∴∠BDF=∠CDE.
在△BDF和△CDE中, 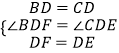 ,
,
∴△BDF≌△CDE(SAS),
∴∠DBF=∠DCE=30°,
即∠DBF的度数不变
(3)解:过点E作EM⊥AB于点M,如图所示.
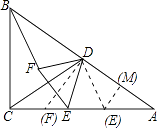
在Rt△ABC中,∠A=30°,AC=6,
∴AB=2BC,AC= ![]() =
= ![]() BC=6,
BC=6,
∴BC=2 ![]() ,AB=4
,AB=4 ![]() .
.
∵△DEF为等边三角形,
∴∠DEF=60°,
∵∠A=30°,
∴∠ADE=30°,
∴DE=AE,
∴AM= ![]() AD=
AD= ![]() ×
× ![]() AB=
AB= ![]() .
.
在Rt△AME中,∠A=30°,AM= ![]() ,
,
∴AE=2EM,AM= ![]() =
= ![]() EM,
EM,
∴EM=1,AE=2,
∴DE=2.
【解析】解:(1)∵在Rt△ABC中,∠C=90°,∠A=30°,
∴AB=2BC,∠CBD=60°.
∵点D是AB中点,
∴BD=BC,
∴△BCD为等边三角形.
所以答案是:等边三角形.
【考点精析】掌握等边三角形的性质和含30度角的直角三角形是解答本题的根本,需要知道等边三角形的三个角都相等并且每个角都是60°;在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两直线AB,CD相交于点O,OE平分∠BOD,∠AOC∶∠AOD=7∶11.
(1)求∠COE的度数;
(2)若OF⊥OE,求∠COF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在△ABC中,D是BC的中点,DE⊥BC,垂足为D,交AB于点E,且BE2-EA2=AC2,
(1)求证:∠A=90°.
(2)若DE=3,BD=4,求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和妹妹做游戏:在一个不透明的箱子里放入20张纸条(除所标字母外其余相同),其中12张纸条上字母为A,8张纸条上的字母为B,将纸条摇匀后任意摸出一张,如果摸到纸条上的字母为A,则小明胜;如果摸到纸条上的字母为B,则妹妹胜.
(1)这个游戏公平吗?请说明理由;
(2)若妹妹在箱子中再放入3张与前面相同的纸条,所标字母为B,此时这个游戏对谁有利? -
科目: 来源: 题型:
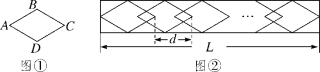
查看答案和解析>>【题目】某工厂沿路护栏的纹饰部分是由若干个和菱形ABCD(如图①)全等的图案组成的,每增加一个菱形,纹饰长度就增加dcm(如图②).已知菱形ABCD的边长为6
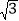 cm,∠BAD=60°.
cm,∠BAD=60°.(1)求AC的长;
(2)若d=15cm,纹饰总长度L为3918cm,则需要多少个这样的菱形图案?
-
科目: 来源: 题型:
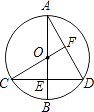
查看答案和解析>>【题目】在⊙O中,直径AB⊥CD于点E,连接CO并延长交AD于点F,且CF⊥AD.求∠D的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=BC,AB=4cm,线段AB上一动点D,以1cm/s的速度从点A出发向终点B运动.过点D作DE⊥AB,交折线AC﹣CB于点E,以DE为一边,在DE左侧作正方形DEFG.设运动时间为x(s)(0<x<4).正方形DEFG与△ABC重叠部分面积为y(cm2).

(1)当x=s时,点F在AC上;
(2)求y关于x的函数解析式,并写出自变量x的取值范围;
(3)设正方形DEFG的中心为点O,直接写出运动过程中,直线BO平分△ABC面积时,自变量x的取值范围.
相关试题

