【题目】如图,抛物线y=ax2+bx﹣3a(a≠0)与x轴交于点A(﹣1,0)和点B,与y轴交于点C(0,2),连接BC.
(1)求该抛物线的解析式和对称轴,并写出线段BC的中点坐标;
(2)将线段BC先向左平移2个单位长度,再向下平移m个单位长度,使点C的对应点C1恰好落在该抛物线上,求此时点C1的坐标和m的值;
(3)若点P是该抛物线上的动点,点Q是该抛物线对称轴上的动点,当以P,Q,B,C四点为顶点的四边形是平行四边形时,求此时点P的坐标.
参考答案:
【答案】
(1)
解:∵抛物线y=ax2+bx﹣3a(a≠0)与x轴交于点A(﹣1,0)和点B,与y轴交于点C(0,2),
∴ ![]() ,
,
解得  .
.
∴抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x+2=﹣
x+2=﹣ ![]() (x﹣1)2+2
(x﹣1)2+2 ![]() ,
,
∴对称轴是x=1,
∵1+(1+1)=3,
∴B点坐标为(3,0),
∴BC的中点坐标为(1.5,1)
(2)
解:∵线段BC先向左平移2个单位长度,再向下平移m个单位长度,使点C的对应点C1恰好落在该抛物线上,
∴点C1的横坐标为﹣2,
当x=﹣2时,y=﹣ ![]() ×(﹣2)2+
×(﹣2)2+ ![]() ×(﹣2)+2=﹣
×(﹣2)+2=﹣ ![]() ,
,
∴点C1的坐标为(﹣2,﹣ ![]() ),
),
m=2﹣(﹣ ![]() )=5
)=5 ![]()
(3)
解:①若BC为平行四边形的一边,
∵BC的横坐标的差为3,
∵点Q的横坐标为1,
∴P的横坐标为4或﹣2,
∵P在抛物线上,
∴P的纵坐标为﹣3 ![]() ,
,
∴P1(4,﹣3 ![]() ),P2(﹣2,﹣3
),P2(﹣2,﹣3 ![]() );
);
②若BC为平行四边形的对角线,
则BC与PQ互相平分,
∵点Q的横坐标为1,BC的中点坐标为(1.5,1),
∴P点的横坐标为1.5+(1.5﹣1)=2,
∴P的纵坐标为﹣ ![]() ×22+
×22+ ![]() ×2+2=2,
×2+2=2,
∴P3(2,2).
综上所述,点P的坐标为:P1(4,﹣3 ![]() ),P2(﹣2,﹣3
),P2(﹣2,﹣3 ![]() ),P3(2,2)
),P3(2,2)
【解析】(1)把点A(﹣1,0)和点C(0,2)的坐标代入所给抛物线可得a、b的值,进而得到该抛物线的解析式和对称轴,再求出点B的坐标,根据中点坐标公式求出线段BC的中点坐标即可;(2)根据平移的性质可知,点C的对应点C1的横坐标为﹣2,再代入抛物线可求点C1的坐标,进一步得到m的值;(3)B、C为定点,可分BC为平行四边形的一边及对角线两种情况探讨得到点P的坐标.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场促销,小鱼将促销信息告诉了妈妈,假设某一商品的定价为
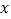 ,并列出不等式为
,并列出不等式为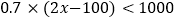 ,那么小鱼告诉妈妈的信息是( )
,那么小鱼告诉妈妈的信息是( )A. 买两件等值的商品可减100元,再打三折,最后不到1000元
B. 买两件等值的商品可打三折,再减100元,最后不到1000元
C. 买两件等值的商品可减100元,再打七折,最后不到1000元
D. 买两件等值的商品可打七折,再减100元,最后不到1000元
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,锐角三角形ABC中,BC>AB>AC,甲、乙两人想找一点P,使得∠BPC与∠A互补,其作法分别如下:
(甲)以A为圆心,AC长为半径画弧交AB于P点,则P即为所求;
(乙)作过B点且与AB垂直的直线,作过C点且与AC垂直的直线,交于P点,则P即为所求.
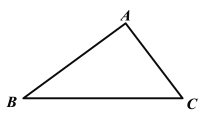
对于甲、乙两人的作法,下列叙述何者正确?( )
A. 两人皆正确
B. 两人皆错误
C. 甲正确,乙错误
D. 甲错误,乙正确
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是大半圆O的直径,AO是小半圆M的直径,点P是大半圆O上一点,PA与小半圆M交于点C,过点C作CD⊥OP于点D.
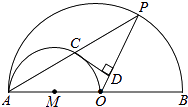
(1)求证:CD是小半圆M的切线;
(2)若AB=8,点P在大半圆O上运动(点P不与A,B两点重合),设PD=x,CD2=y. ①求y与x之间的函数关系式,并写出自变量x的取值范围;
②当y=3时,求P,M两点之间的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠ABC=45°,D是BC边上的一点,BD=2,将△ACD沿直线AD翻折,点C刚好落在AB边上的点E处.若P是直线AD上的动点,则△PEB的周长的最小值是________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题
(1)计算: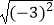 ﹣(
﹣(  )﹣1+(π﹣
)﹣1+(π﹣ 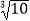 )0﹣(﹣1)100;
)0﹣(﹣1)100;
(2)已知|a+1|+(b﹣3)2=0,求代数式( ﹣
﹣ 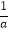 )÷
)÷ 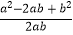 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.

相关试题

