【题目】如图1,等边△ABC的边长为4cm,动点D从点B出发,沿射线BC方向移动,以AD为边作等边△ADE.
(1)在点D运动的过程中,点E能否移动至直线AB上?若能,求出此时BD的长;若不能,请说明理由;
(2)如图2,在点D从点B开始移动至点C的过程中,以等边△ADE的边AD、DE为边作ADEF.
①ADEF的面积是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由;
②若点M、N、P分别为AE、AD、DE上动点,直接写出MN+MP的最小值.
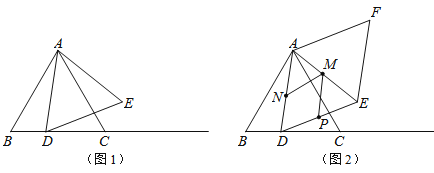
参考答案:
【答案】(1)不存在;(2)①存在,6![]() ;②3.
;②3.
【解析】试题分析:(1)根据等边三角形的性质可知: ![]() 由三角形外角的性质可知
由三角形外角的性质可知![]() 从而可知:
从而可知: ![]() 所以
所以![]() 点E不能移动到直线AB上.
点E不能移动到直线AB上.
(2)因为△ADE的面积![]() 所以当AD最短时,△ADE的面积有最小,根据垂线段最短可知当AD⊥BC时,△ADE的面积最小.四边形
所以当AD最短时,△ADE的面积有最小,根据垂线段最短可知当AD⊥BC时,△ADE的面积最小.四边形![]() 为平四边形,AE为对角线,所以平行四边形
为平四边形,AE为对角线,所以平行四边形![]() 的面积是△ADE面积的2倍,所以△ADE的面积最小时,平行四边形的面积最小;
的面积是△ADE面积的2倍,所以△ADE的面积最小时,平行四边形的面积最小;
(3)当点N、M、P在一条直线上,且NP⊥AD时,MN+MP有最小值,最小值为AD与EF之间的距离.
试题解析:(1)不存在.
理由:如图1所示:
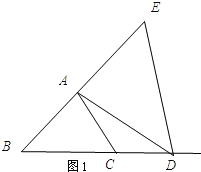
∵△ABC和△ADE均为等边三角形,
∴![]()
∵![]()
∴![]()
又∵![]()
∴![]()
∴点E不能移动到直线AB上.
(2)①存在:在图(2)中,当AD⊥BC时,△ADE的面积最小.

在Rt△ADB中, ![]()
∴△ADE的面积![]()
∵四边形ADEF为平四边形,AE为对角线,
∴平行四边形ADEF的面积是△ADE面积的2倍.
∴ADEF的面积的最小值![]()
②如图3所示:作点P关于AE的对称点P1,
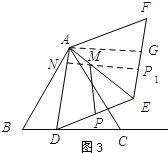
当点N、M、P在一条直线上,且NP⊥AD时,MN+MP有最小值,
过点A作AG∥NP1,
∵AN∥GP1,AG∥NP,
∴四边形ANP1G为平行四边形.
∴![]()
即MN+MP的最小值为3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的方法拼成一个边长为(m+n)的正方形.
⑴ 请用两种不同的方法求图2中阴影部分的面积.
方法1: ;方法2: ;
⑵ 观察图2写出
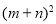 ,
,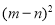 ,
,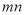 三个代数式之间的等量关系: ;
三个代数式之间的等量关系: ;⑶ 根据⑵中你发现的等量关系,解决如下问题:若
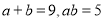 ,求
,求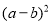 的值.
的值.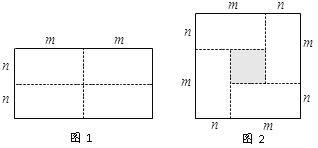
-
科目: 来源: 题型:
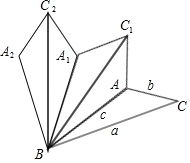
查看答案和解析>>【题目】在△ABC中,∠ABC<20°,三边长分别为a,b,c,将△ABC沿直线BA翻折,得到△ABC1;然后将△ABC1沿直线BC1翻折,得到△A1BC1;再将△A1BC1沿直线A1B翻折,得到△A1BC2;…,若翻折4次后,得到图形A2BCAC1A1C2的周长为a+c+5b,则翻折11次后,所得图形的周长为_____________.(结果用含有a,b,c的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公大楼顶端A测得旗杆顶端E的俯角α是45°,旗杆低端D到大楼前梯砍底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:
 ,则大楼AB的高度为_________米.
,则大楼AB的高度为_________米.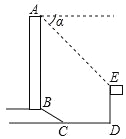
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是(A,B)的好点.
例如,如图1,点A表示的数为-1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的好点;
又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是(A,B)的好点,但点D是(B,A)的好点.
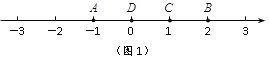
知识运用:
⑴ 如图1,点B是(D,C)的好点吗? (填是或不是);
⑵ 如图2,A、B为数轴上两点,点A所表示的数为-40,点B所表示的数为20.现有一只电子蚂蚁P从点B出发,以2个单位每秒的速度向左运动,到达点A停止.当t为何值时,P、A和B中恰有一个点为其余两点的好点?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,Rt△ABC中,∠B=90°,∠CAB=30°,它的顶点A的坐标为(10,0),顶点B的坐标为(5,5
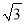 ),AB=10,点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,设运动的时间为t秒.
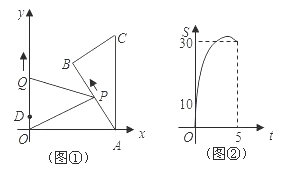
),AB=10,点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,设运动的时间为t秒.(1)当点P在AB上运动时,△OPQ的面积S(平方单位)与时间t(秒)之间的函数图象为抛物线的一部分,(如图②),则点P的运动速度为 ;
(2)求(1)中面积S与时间t之间的函数关系式及面积S的最大值及S取最大值时点P的坐标;
(3)如果点P,Q保持(1)中的速度不变,那么点P沿AB边运动时,∠OPQ的大小随着时间t的增大而增大;沿着BC边运动时,∠OPQ的大小随着时间t的增大而减小,当点P沿这两边运动时,使∠OPQ=90°的点P有 个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两仓库分别有水泥20吨和30吨,C、D两工地分别需要水泥15吨和35吨.已知从A、B仓库到C、D工地的运价如下表:
到C工地
到D工地
A仓库
每吨15元
每吨12元
B仓库
每吨10元
每吨9元
(1)若从A仓库运到C工地的水泥为
 吨,则用含x的代数式表示从A仓库运到D工地的水泥为 吨,从B仓库将水泥运到D工地的运输费用为 元;
吨,则用含x的代数式表示从A仓库运到D工地的水泥为 吨,从B仓库将水泥运到D工地的运输费用为 元;(2)求把全部水泥从A、B两仓库运到C、D两工地的总运输费(用含
 的代数式表示并化简);
的代数式表示并化简);(3)如果从A仓库运到C工地的水泥为15吨时,那么总运输费为多少元?
相关试题

