Question

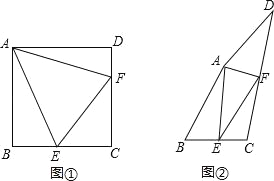
【题目】探究：如图①，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连结EF，求证：EF=BE+DF．

应用：如图②，在四边形ABCD中，点E、F分别在BC、CD上，AB=AD，∠B+∠D=90°，∠EAF=∠BAD，若EF=3，BE=2，则DF= ．

Answer 1

【答案】(1)证明见解析；（2）．

【解析】

试题分析：（1）如图①中，把△ABE绕点A逆时针旋转90°得到△ADE′，只要证明△AFE≌△AFE′即可解决问题．

（2）如图②中，将△ABE绕点A旋转到△ADE′位置连接E′F．，只要证明△FAE≌△FAE′得EF=FE′，在RT△E′DF中利用勾股定理即可解决问题．

试题解析：（1）如图①中，

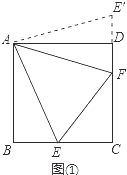
在正方形ABCD中，∵AB=AD，∠BAD=∠ADC=∠B=90°，

把△ABE绕点A逆时针旋转90°得到△ADE′，

∵∠ADF=∠ADE′=90°，

∴点F、D、E′共线，

∴∠E′AF=90°-45°=45°=∠EAF，

在△AFE和△AFE′中，

，

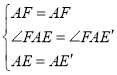∴△AFE≌△AFE′，

∵EF=FE′=DE′+DF=DE+DF．

（2）如图②中，

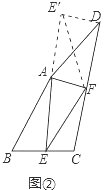
因为AB=AD，所以可以将△ABE绕点A旋转到△ADE′位置，连接E′F．

∵∠B+∠ADF=90°，∠B=∠E′DA，

∴∠E′DF=∠E′DA+′ADF=90°，

∵∠BAE+∠DAF=∠EAF，∠E′AD=∠BAE，

∴∠E′AF=∠EAF，

在△FAE和△FAE′中，

，

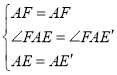∴△FAE≌△FAE′，

∴EF=FE′=3，

在RT△E′DF中，∵∠E′DF=90°，E′F=3，DE′=BE=2，

∴DF=．