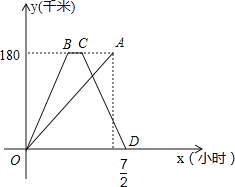
【题目】快、慢两车分别从相距180千米的甲、乙两地同时出发,沿同一路线匀速行驶,相向而行,快车到达乙地停留一段时间后,按原路原速返回甲地.慢车到达甲地比快车到达甲地早![]() 小时,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(千米)与所用时间x(小时)的函数图象如图所示,请结合图象信息解答下列问题:
小时,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(千米)与所用时间x(小时)的函数图象如图所示,请结合图象信息解答下列问题:
(1)请直接写出快、慢两车的速度;
(2)求快车返回过程中y(千米)与x(小时)的函数关系式;
(3)两车出发后经过多长时间相距90千米的路程?
参考答案:
【答案】(1)快车、慢车速度分别为120千米/时,60千米/时;(2)y=﹣120x+420(2≤x≤![]() );(3)两车出发后经过
);(3)两车出发后经过![]() 或
或![]() 或
或![]() 小时相距90千米的路程
小时相距90千米的路程
【解析】试题分析:(1)根据路程与相应的时间,求得慢车的速度,再根据慢车速度是快车速度的一半,求得快车速度;
(2)先求得点C的坐标,再根据点D的坐标,运用待定系数法求得CD的解析式;
(3)分三种情况:在两车相遇之前;在两车相遇之后;在快车返回之后,分别求得时间即可.
试题解析:
(1)快车速度:180×2÷(![]() )=120千米/时,
)=120千米/时,
慢车速度:120÷2=60千米/时;
(2)快车停留的时间:![]() ﹣
﹣![]() ×2=
×2=![]() (小时),
(小时),
![]() +
+![]() =2(小时),即C(2,180),
=2(小时),即C(2,180),
设CD的解析式为:y=kx+b,则
将C(2,180),D(![]() ,0)代入,得
,0)代入,得
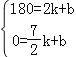 ,
,
解得![]() ,
,
∴快车返回过程中y(千米)与x(小时)的函数关系式为y=﹣120x+420(2≤x≤![]() );
);
(3)相遇之前:120x+60x+90=180,
解得x=![]() ;
;
相遇之后:120x+60x﹣90=180,
解得x=![]() ;
;
快车从甲地到乙地需要180÷120=![]() 小时,
小时,
快车返回之后:60x=90+120(x﹣![]() ﹣
﹣![]() )
)
解得x=![]()
综上所述,两车出发后经过![]() 或
或![]() 或
或![]() 小时相距90千米的路程.
小时相距90千米的路程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. a2a3=a6 B. 2a+3b=5ab C. a8÷a2=a6 D. (a2b)2=a4b
-
科目: 来源: 题型:
查看答案和解析>>【题目】把命题“三个角都相等的三角形是等边三角形”改写成“如果……,那么……”的形式为 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(x0,y0)和直线y=kx+b,则点P到直线y=kx+b的距离证明可用公式d=
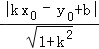 计算.
计算.例如:求点P(﹣1,2)到直线y=3x+7的距离.
解:因为直线y=3x+7,其中k=3,b=7.
所以点P(﹣1,2)到直线y=3x+7的距离为:d=
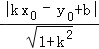 =
=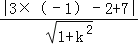 =
=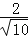 =
= .
.根据以上材料,解答下列问题:
(1)求点P(1,﹣1)到直线y=x﹣1的距离;
(2)已知⊙Q的圆心Q坐标为(0,5),半径r为2,判断⊙Q与直线y=
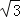 x+9的位置关系并说明理由;
x+9的位置关系并说明理由;(3)已知直线y=﹣2x+4与y=﹣2x﹣6平行,求这两条直线之间的距离.
-
科目: 来源: 题型:
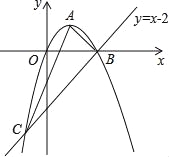
查看答案和解析>>【题目】(2016广西省南宁市第24题)如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x﹣2交于B,C两点.
(1)求抛物线的解析式及点C的坐标;
(2)求证:△ABC是直角三角形;
(3)若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
 ×(-
×(- );
);(2)(-
 )×(-
)×(- );
);(3)-2
 ×25;
×25; (4)(-0.3)×(-1
 );
);(5)-2×3×(-4);
(6)-6×(-5)×(-7);
(7)0.1×(-0.001)×(-1);
(8)(-100)×(-1)×(-3)×(-0.5);
(9)(-17)×(-49)×0×(-13)×37;
(10)(-4
 )×1.25×(-8);
)×1.25×(-8);(11)(-10) ×(-8.24) ×(-0.1);
(12)-
 ×2.4×
×2.4× ;
;(13)71
 ×(-8).
×(-8). -
科目: 来源: 题型:
查看答案和解析>>【题目】如果单项式x2ym+2与xny的和仍然是一个单项式,则m、n的值是( )
A.m=2,n=2
B.m=﹣1,n=2
C.m=﹣2,n=2
D.m=2,n=﹣1
相关试题

