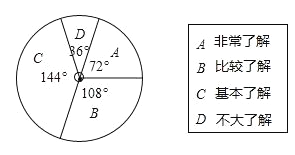
【题目】(2016浙江省温州市第18题)为了解学生对“垃圾分类”知识的了解程度,某学校对本校学生进行抽样调查,并绘制统计图,其中统计图中没有标注相应人数的百分比.请根据统计图回答下列问题:
(1)求“非常了解”的人数的百分比.
(2)已知该校共有1200名学生,请估计对“垃圾分类”知识达到“非常了解”和“比较了解”程度的学生共有多少人?
参考答案:
【答案】(1)、20%;(2)、600
【解析】
试题分析:(1)、根据扇形统计图可以求得“非常了解”的人数的百分比;(2)、根据扇形统计图可以求得对“垃圾分类”知识达到“非常了解”和“比较了解”程度的学生共有多少人.
试题解析:(1)、由题意可得,
“非常了解”的人数的百分比为:![]() , 即“非常了解”的人数的百分比为20%;
, 即“非常了解”的人数的百分比为20%;
(2)、由题意可得,
对“垃圾分类”知识达到“非常了解”和“比较了解”程度的学生共有:1200×![]() =600(人),
=600(人),
即对“垃圾分类”知识达到“非常了解”和“比较了解”程度的学生共有600人
-
科目: 来源: 题型:
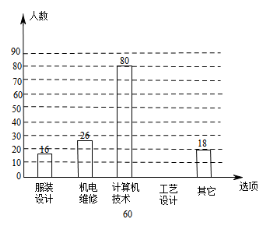
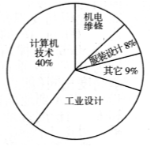
查看答案和解析>>【题目】(2016山西省第18题)每年5月的第二周为:“职业教育活动周”,今年我省展开了以“弘扬工匠精神,打造技能强国”为主题的系列活动,活动期间某职业中学组织全校师生并邀请学生家长和社区居民参加“职教体验观摩”活动,相关职业技术人员进行了现场演示,活动后该校随机抽取了部分学生进行调查:“你最感兴趣的一种职业技能是什么?”并对此进行了统计,绘制了统计图(均不完整).
(1)补全条形统计图和扇形统计图;
(2)若该校共有1800名学生,请估计该校对“工业设计”最感兴趣的学生有多少人?
(3)要从这些被调查的学生中随机抽取一人进行访谈,那么正好抽到对“机电维修”最感兴趣的学生的概率是
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据分为5组,第一组的频率为0.15,第二组的频率为0.21,第三组的频率为0.29,第四组的频率为0.15,则第五组的频率是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=52°,∠ABC与∠ACB的角平分线交于D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,∠ABD4与∠ACD4的角平分线交于点D5,则∠BD5C的度数是( )
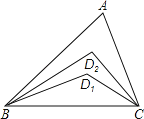
A. 56° B. 60° C. 68° D. 94°
-
科目: 来源: 题型:
查看答案和解析>>【题目】用10米长的铝材制成一个矩形窗框,使它的面积为6平方米.若设它的一条边长为x米,则根据题意可列出关于x的方程为( )
A.x(5+x)=6
B.x(5﹣x)=6
C.x(10﹣x)=6
D.x(10﹣2x)=6 -
科目: 来源: 题型:
查看答案和解析>>【题目】248﹣1能被60~70之间的两个整数整除,这两个整数是
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016云南省第21题)某超市为庆祝开业举办大酬宾抽奖活动,凡在开业当天进店购物的顾客,都能获得一次抽奖的机会,抽奖规则如下:在一个不透明的盒子里装有分别标有数字1、2、3、4的4个小球,它们的形状、大小、质地完全相同,顾客先从盒子里随机取出一个小球,记下小球上标有的数字,然后把小球放回盒子并搅拌均匀,再从盒子中随机取出一个小球,记下小球上标有的数字,并计算两次记下的数字之和,若两次所得的数字之和为8,则可获得50元代金券一张;若所得的数字之和为6,则可获得30元代金券一张;若所得的数字之和为5,则可获得15元代金券一张;其他情况都不中奖.
(1)请用列表或树状图(树状图也称树形图)的方法(选其中一种即可),把抽奖一次可能出现的结果表示出来;
(2)假如你参加了该超市开业当天的一次抽奖活动,求能中奖的概率P.
相关试题

